研究内容

地球内部不均質媒体中の波動場解析

任意の異方性と分散性のある不均質媒体中の波動場を計算することは物理探査、地震防災、構造物健全性評価などさまざまな方面で重要であるが、現在のほとんどの理論は、限られた時間内で限られた能力の計算装置を用いて、当座の目的を達する計算方式が採用されていて、分散性波動を本格的に扱えるものは少ない。本研究では、媒質の物性の周波数依存性を正確に反映する計算手法として、通常の波動解析でよく使われている時間領域法ではなく、周波数領域法が適切と考えて構成した新しい手法を開発した。現在計算コードを作成し、実用性・有用性を検証している。

波動を伝播する媒体は、内部にどのような不連続を含もうとも時間tと空間xの関数である励起e(t,x)と波動場W(t,x)とは比例する線形力学系である。波動方程式は、波動場の入力に対する出力が励起を与える形式になっている。そこで、これを逆解きして、励起を入力、波動場を出力とする線形力学系としての応答特性（周波数・波数応答関数）を導く。物性定数に不連続のある点では微分ができないから、通常は、境界として条件設定をするなどの扱いをするが、この理論では全ての不連続を、ステップ関数を基底とする超関数列を使い、変位の連続性は保持して全ての点で微分操作をできるようにする。

本計算理論の概要は以下のとおりである。波動方程式を周波数領域で表現すると(1)のようになる。
D(ω,x)W(ω,x)=e(ω,x) … (1)
ただし、３次元でも基本はかわらないので簡単のため１次元で表現してある。これは角周波数ωと空間xに関する支配方程式で、各点における励起と波動の関係を表している。D(ω,x)はωとxに関する微分演算子を表す。これらをWの連立方程式として解くため、(1)に対してxに関する離散フーリエ変換を行うと(1)の左辺は波数kとk'の畳み込み積Σ_kD(ω,k,k'-k)W(ω,k)になる。kとk'の配列を整理し、畳み込みを行列演算として表現すると、次のようにW(ω,k)の連立１次方程式になる。
D(ω,k',k)W(ω,k)=e(ω,k') … (2)
そこで、D(ω,k',k)の逆行列をR(ω,k',k)と書いて、(2)は直ちにWを次のように与える。
W(ω,k)=R(ω,k,k')e(ω,k') … (3)
かくして、励起に比例する波動場が求まる。ここでR(ω,k,k')を周波数・波数応答関数とよぶ。

この手法では、立方離散空間グリッドシステムの間隔Δxできまるナイキスト波数k_Nまでの領域で、任意の不均質媒体中の任意の励起によって生じる波動場をグリッド分散など系統的偏差なく計算できる。また、周波数依存性をもつ任意に複雑な構造について波動場が精密に計算できるため適用範囲は多岐にわたり、実用性は高い。また、電磁波と弾性波に共通に適用できるため高い汎用性がある。

本理論はあまりにも簡単なのでその妥当性が疑われたが、１次元系での数値計算によって理論の妥当性は確認された。しかしながら、現実の波動計算への実用については、２次元、３次元への拡張にあたって計算時間短縮の観点から最適アルゴリズムの確立が最重要課題であることが明らかとなった。現在本手法の確立に向けて検討を行っている。

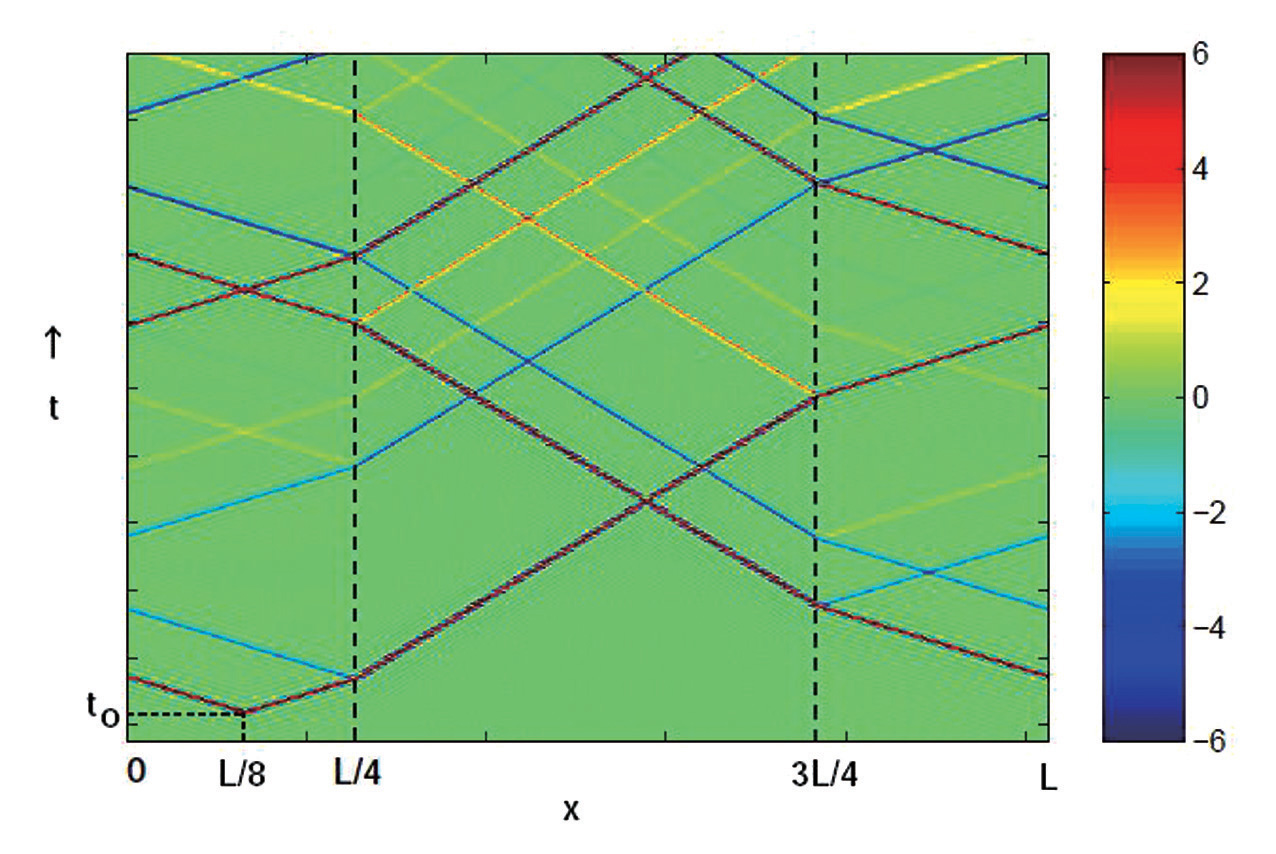
図は本手法を用いて１次元弾性体における粒子速度の走時曲線を示したものである。長さLの１次元不均質媒質で、位置x=L/4およびx=3L/4に不連続を置き、x=0,Lに周期的境界条件を与えた。波動の励起にはt=t₀、x=L/8において撃力を与えている。不連続点における反射および屈折が観察され、時間が十分に経過してもグリッド分散のない波動場が得られた。また、不連続点での応力の連続も確認し、数値的に得られる解析解と十分な精度で一致することを検証した。