Current Research

Analysis of Wave Fields in the Earth's Interior with Heterogeneous Structure

Our major concern in Solid Earth Geophysics is structure exploration and state monitoring within the earth's crust and in particular, around tectonically active areas. Our most significant social responsibility is to discover a better way to mitigate disasters, which originate from such tectonic events as earthquakes, by understanding their nature. We recognized the necessity of such a code that enables us to compute wave fields in arbitrary structure that simulates the earth's interior. Whereas there are a number of codes that calculate wave fields under various conditions, very few satisfactory ones compute wave field within a limited part of a large body with the most general structures in the frequency domain. Therefore, we have proposed a new method for calculating wave fields in generally anisotropic, dispersive, and heterogeneous media to provide theoretical support for geophysical exploration and also a potential analysis tool of very accurate data acquired by ACROSS, an active monitoring system of the earth's interior proposed by a Japanese research group. Numerical validation of the method and development of practical code are underway.

Keeping possible extensions to general cases in mind, we examined the basic nature of this theory in the simplest case : a finite one-dimensional elastic body. Spatial variation of material parameters in the wave equation is converted to a set of several quantities that separately represent the continuity and the discontinuity of different orders as a function of space in the use of hyperfunctions. With a set of converted parameters, the wave equation described by differential equation is rewritten to a linear system model expressing external excitation as output and wave field as input, where the contribution from discontinuity is brought to a self-excitation term containing impedance contrasts at the discontinuities. This linear equation is converted to an inverse system model expressing external excitation as input and wave field as output in frequency and wavenumber domains. The inverse system model is represented by FWR, the frequency and wavenumber response characteristics. Multiplying FWR by excitation, we obtain wave field that represents a dispersion relation. Consequently, no computational procedures are required in dealing with the boundary conditions at discontinuities in the medium, and it is free from grid dispersion.

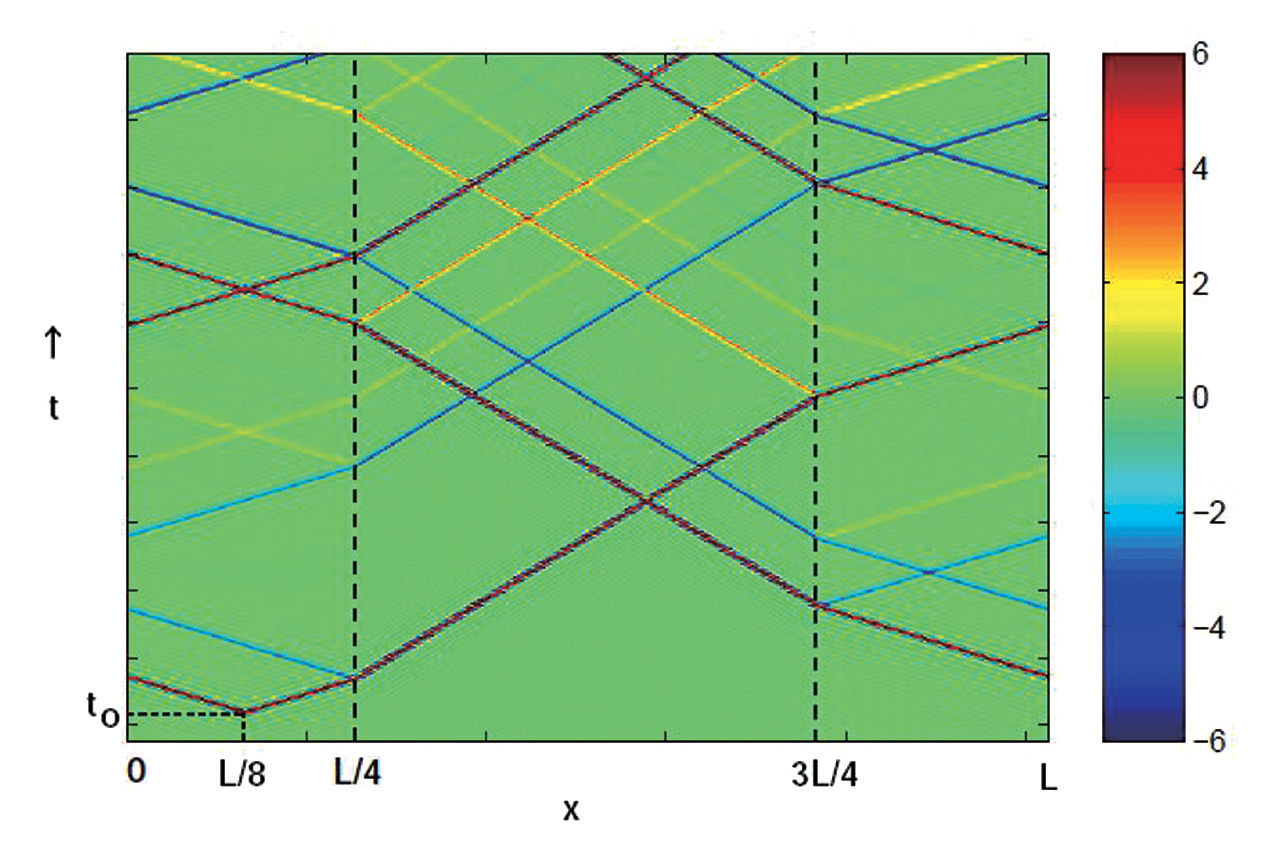
We calculated a one- dimensional case with two uniform media to validate the present theory. Consider a circular elastic body with length L consisting of two segments whose physical properties are different from each other and are in contact with discontinuities at x=L/4 and 3L/4. Impulsive excitation is given at a point of t=t0 and x=L/8. The figure shown here demonstrates the validity of the theory. We can observe that the two impulses start to propagate leftward and rightward, respectively, exactly from the set point of initial excitation at t=t0 and x=L/8. Then the waves repeatedly propagate both with reflection at and with transmission through discontinuity points x=L/4 and 3L/4.

One important point of the current theory is its simple structure. Furthermore, the theory is expected to be applied commonly to both elastic and electromagnetic waves in any heterogeneous medium with anisotropy and frequency dependent properties.