研究内容

モデリングと最適化の数理

■研究の概要■
自然界や人工物のマクロな現象の多くはある程度の単純化を行えば数式でモデル化することができる。例えば、固体や流体の変形、音や熱の伝わる現象など、我々が日常的に見たり感じたりすることのできる現象の多くは偏微分方程式の境界値問題としてモデル化される。このような問題に対する数値解は、計算機と数値解析に関する理論の発達により得られるようになってきた。それらの結果は、コンピュータグラフィックスの発展に支えられて、可視化され、コンピュータシミュレーションとして広く認知されるようになってきた。
現象のシミュレーションから現象の制御・最適化へ：コンピュータシミュレーションのこれまでの発達が、もっぱら現象を忠実に再現することに主眼が置かれていたことに対して、私の研究室では、現象が望みの現象になるように形や材質を制御する、あるいはある目的に対して形や材質を最適化する問題に取り組んでいる。
■典型的な問題■
簡単な形状最適化問題を示そう。 を  次元のある有界領域とする。ここで、領域変動を表す写像  を設計変数に選ぶ。 が与えられたならば、 上である現象が



を満たす  によって決定されるとする。ここで、 は与えられている関数と仮定する。さらに、

を評価関数と定義する。このとき、



を満たす を求める問題を形状最適化問題という。このような問題に対して、私の研究室では、関数空間の勾配法に基づく独自の解法を提案している。
■人工物設計への応用■
例えば、力を受けたときの変形が最も少ない物体の形は、弾性変形に対する偏微分方程式の境界値問題を使い、目的関数に外力仕事、制約関数に体積を用いた不等式条件を考えれば、解くことができる。流れの中で抵抗が最も少なくなる物体の形なども同様に解くことができる。これらの基本的な形状最適化問題に対しては、製品設計の現場で使えるレベルに達している(図左側参照)。
■医療・福祉への応用■
人間を含めた生体の形もマクロな現象との関わりで作り出されていることが少なくない。私の研究室では、コンピュータシミュレーションの手法を生体の形や疾患の解明、さらには治療法の評価および最適化、福祉機器の設計などに役立てることを目指している。
■最近の研究テーマ■
1. 形状最適化問題における特異点まわりの形状微分について
2. ブレーキ鳴きに対する形状最適化
3. 静電容量式センサに対する形状最適化
4. 振動固有対を用いた建築物の損傷同定
5. 粒子法による流れ場の形状最適化
6. リンク機構の形状最適化
7. 医用データに基づく患者別数値モデルの作成法
■今後の展開■
現象のモデリングと最適化に関する研究を進めていく上で、原理を追求すれば数学としての厳密性を問われ、実用を考えれば工学としての汎用性を求められ、医療・福祉への応用を目指せば、医学としての要求に応えなければならない。これらの目標を達成するためには、異分野の専門家との協働が欠かせない。いろいろな出会いを大事にしていきたい。

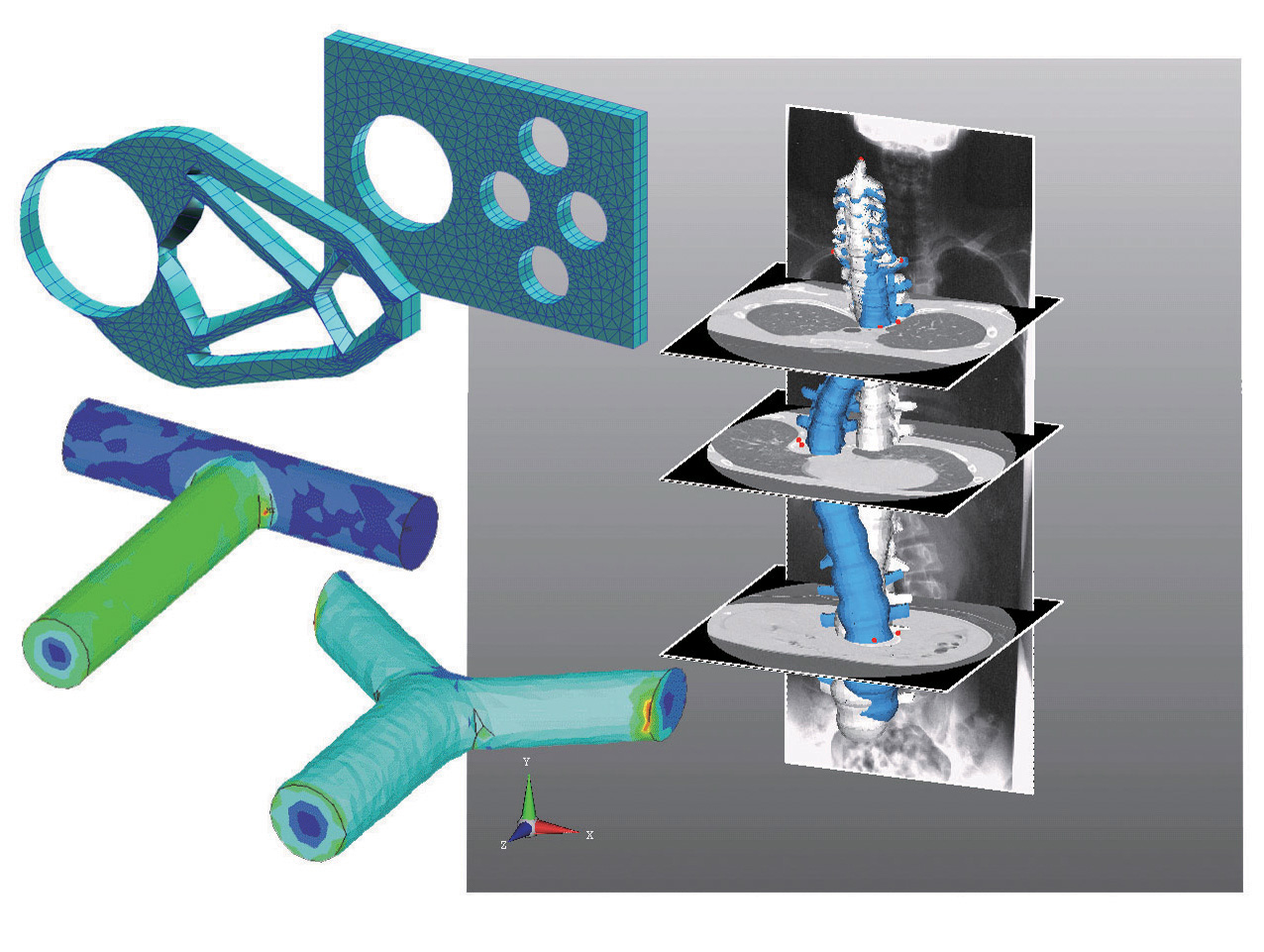
弾性体・流れ場の最適化／脊柱特発性側彎症患者別モデリング