Current Research

Mathematics of Modeling and Optimization

OUTLINE
Most macroscopic phenomena in nature and artificial products can be represented with mathematical equations by simplifying phenomena in some senses. Phenomena seen or felt in daily life, such as the deformation of solids and fluids or the propagation of sound and heat, are expressed with solutions to boundary value problems of partial differential equations. Numerical solutions to these problems have come to be obtained by the progress of computer technology and theory of numerical analysis. These results are visualized by the progress of computer graphics and have come to be widely recognized as computer simulation.
FROM THE SIMULATION OF PHENOMENA TO THE OPTIMIZATION OF PHENOMENA : While recent progress of computer simulation has aimed to faithfully realize the phenomena, our laboratory has been tackling the control or optimization problems of shapes and material to realize the wished for phenomena.
TYPICAL PROBLEM
A simple shape optimization problem can be shown as follows. Let  be a -dimentional bounded domain. Here, we choose a map representing domain variation as design variable. If is given, a phenomenon in is determined as the solution to

,

where is a given function. Moreover, we defined

as cost functions. Baed on the definitions, we call finding problem of such that、



a shape optimization problem. For the problem, we proposed a solution based on the gradient method in function space.
APPLICATIONS TO PRODUCT DESIGN
For instance, a shape optimization problem of a solid that minimizes deformation under external force can be solved by setting the elastic equations for the boundary value problem, the external work for the objective functional, and adding a volume constraint. Shape optimization of a solid in a flow field and similar problems can be solved in the same way. For these fundamental shape optimization problems, our method has been put to practical use in product design (see left side of the figure).
APPLICATIONS TO MEDICAL CARE AND WELFARE
It is not rare that macroscopic phenomena involve the shapes of living bodies including human beings. We are promoting the use of computer simulation techniques and optimization to understand the shapes of living bodies, the mechanisms of diseases, and to improve medical treatments and the design of welfare instruments.
RECENT TOPICS
1. On shape derivative around singular point in shape optimization problem
2. Shape optimization for brake squeal
3. Shape optimization of electrostatic capacitive sensor
4. Damage identification in building using vibration eigen pair
5. Shape optimization for flow field by particle method
6. Shape optimization for a link mechanism
7. Construction method of numerical models for individual patients based on medical data
FUTURE DEVELOPMENTS
To develop studies on the modeling and optimization of phenomena, when pursuing such principles, mathematical rigor is inquired ; when considering practical uses, engineering conveniences are required, and when aiming for medical care and welfare applications, we have to comply with medicine's demands. To achieve such objectives, collaboration with specialists working in different disciplines is crucial. We contemplate a great deal of all sorts of encounters.

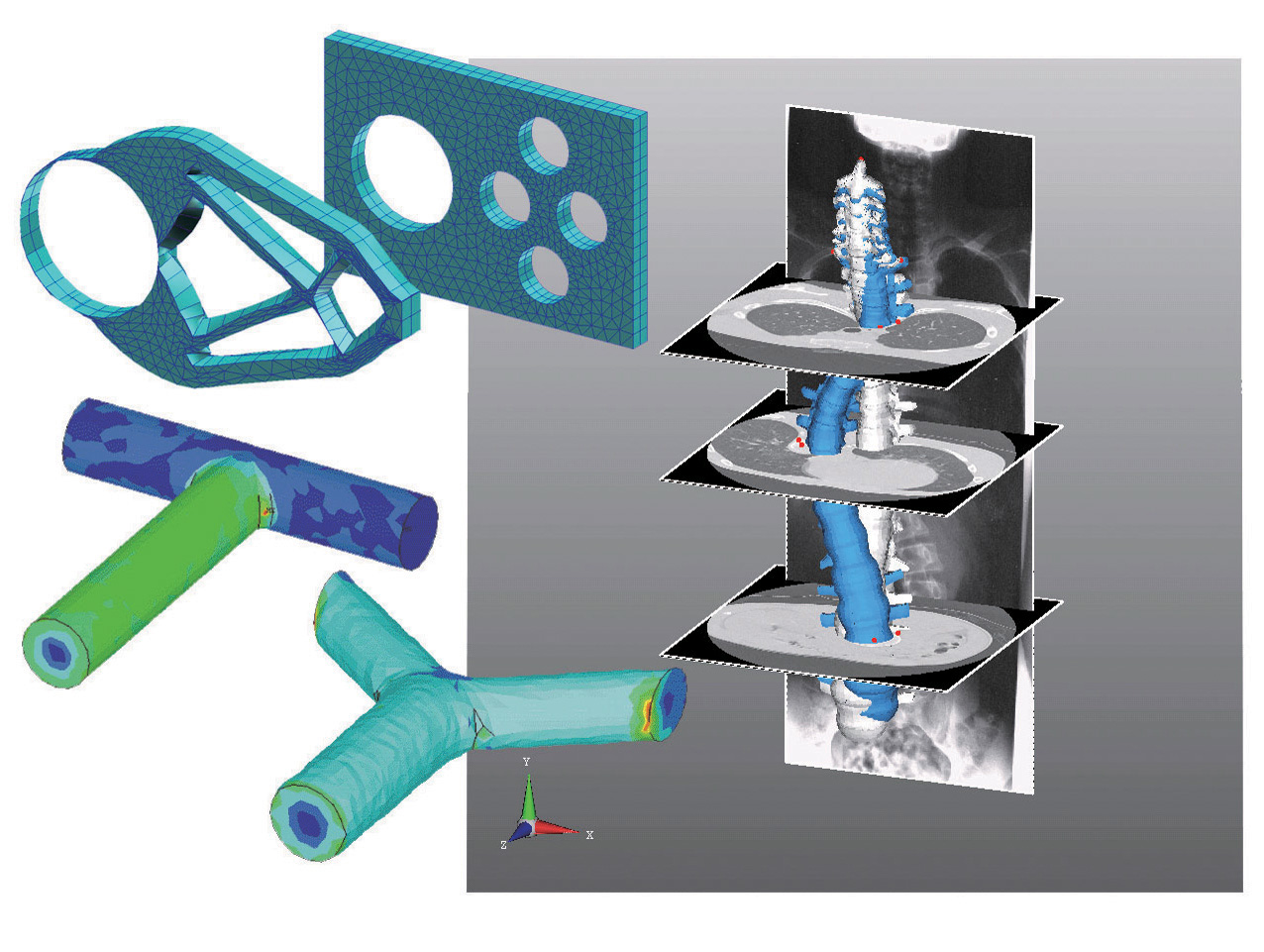
Figure : Optimization of elastic body and flow field/Individual modeling of scoliosis