研究内容

円分体の理論とBernoulli数の研究

整数論における最も重要な概念の一つが類数である。類数が１でないことが、おきうる事に気が付いたときから代数的整数論が始まったといっても過言ではない。abel体の場合はDirichletの解析的類数公式により一応のexplicitな表示はあるものの、それによりただちに値が評価できるというものではない。また、いくつかの狭いクラスに対して類数の挙動・振る舞い・整除性などが解っているが、その背後に潜むであろう理論にまで深く言及されているものは、一つ例外を除いて存在しない。その例外のクラスとは、正に、円分体であり、その理論とは岩澤理論のことである。岩澤理論は現在もなお発展し、一般化されている理論である。最近ではFermat予想の解決にも大きく関わってきた。しかしながら、さらなる発展を望むとすれば、そこには一つ超えなければならない大きな壁がある。それがBernoulli数である。Bernoulli数が歴史の表舞台に登場してくるのは、1850年にKummerが証明した：
『正則素数に対してFermatの予想は正しい。』
という判定法からであろう。今となってはWilesによってFermat予想は完全に解かれてしまっている訳であるから、この判定法自身は多少色あせたものになってしまったといわざるをえない。しかしFermat予想が逆にBernoulli数に対して重要な情報を与えるものではない。そしてBernoulli数の重要性をいささかでも揺るがすというものでは決してない。その外にもBernoulli数は、数多くの重要な数学的概念の判定法に登場してくる魅惑的な数なのである。この数を征服することなくして整数論の完成はありえないのである。Bernoulli数へのアプローチの一つにq-analogueとよばれる手法がある。これは通常の1,2,3…という数を扱うのではなく変数qを一つ決めて[1]=1,[2]=1＋q,[3]=1＋q＋q²…という数を扱うのである（q→1とすれば通常の数にもどることを注意しておく）。これらの数は通常の数と密接な関係にあり、多くの公式が、そのまま奇麗な形で、この数に対しても成立することが解っている。Bernoulli数に対してもq-Bernoulli数とよばれる数が定義されていて、ほとんどの公式のq-analogueが証明されている。このような数を扱う理由の一つは、qの大きさを適当に制限して議論をしておき最後にq→1という極限操作を行うと通常は発見困難な公式が得られたり、通常は困難な証明が簡易化されたりすることが多々あるためである。しかし、数論においてはq-analogueが構成されている対象が余りに少なすぎ、未だqの世界で議論を展開する段階ではない。さらに、何が数論にとって意味のあるq-analogueなのか、その示唆を与える重要な例も見つかっていない。以上の様な理由から、より多くの対象に対して体系的にq-analogueを構成することは意味の有ることであり、その中から真に意味の有るものを見い出すことが重要である。[2]（1992）の中で全く新しい考え方に基づくq-analogueの構成法が導かれた。この構成法により、これまではそれぞれ個別に定義されていたq-analogueが体系的に定義できる道がひらかれた。さらに、最近この構成法が形式群と深く結びついていること、すなわち、より自然な形でこの構成法が通常の世界とqの世界を結び付けていることが判明した。この形式群を糸口にしてq-analogueの理論を展開したいと考えている。数論におけるqの世界の環境整備を目的とし、最終的には新しいBernoulli数の関係式の発見を目標とする。
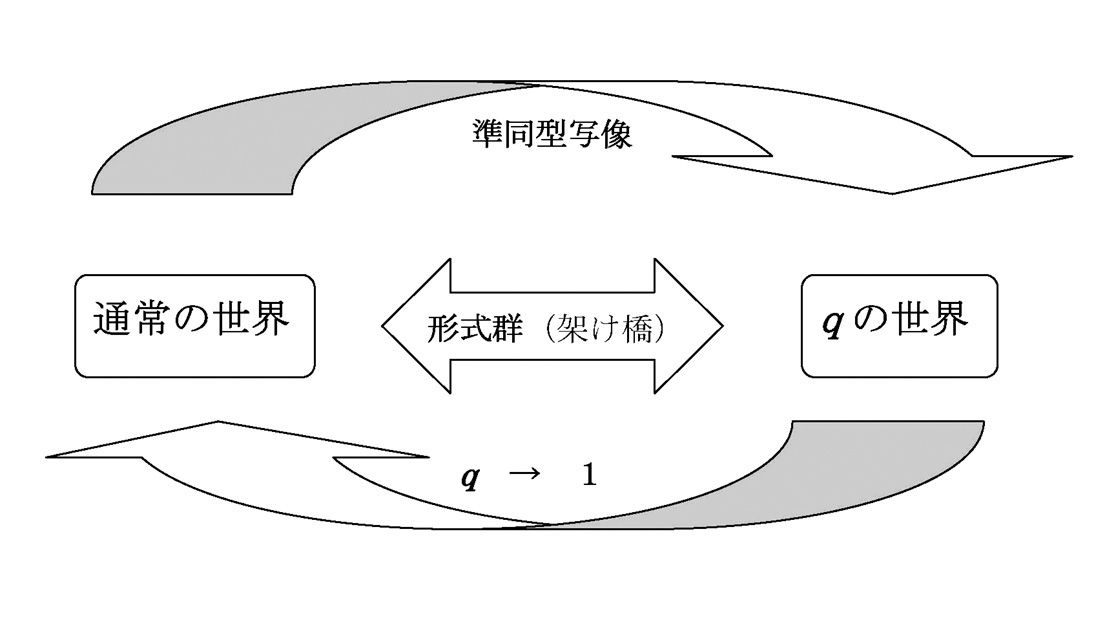
数論におけるq-analogueの理論は1940年代後半にL. Carlitzにより創始されたが、その例は、少なく統一的な議論を展開できる状況ではなかった。そこで、我々は、ある種の冪級数に対してそのq-analogueが定義できることを証明し、多くの新しいq-analogueの関係式を発見した。その理論とはL. Carlitzが定義したq-Bernoulli数およびq-Euler数に基礎を置き、それをもとに、通常の世界からqの世界への同形写像（q-operatorと言う）を具体的に構成し、その像として一般のq-analogueの定義がなされ、その同形性によって、新しい公式、および、非常に煩雑であったq-Bernoulli数、q-Euler数に関する様々な公式の別証明等が古典的な公式からの帰結として容易に得ることができるというものである。すなわちL. Carlitzの理論は、通常の世界からの極自然な帰結として捉えるとこができるわけである。さらに、形式群の概念を用いることにより、上のようなq-analogueの構成が必然性をもつことが判明した。