Comprehensive List of Researchers "Information Knowledge"
Department of Computer Science and Mathematical Informatics
- Name
- SATOH, Junya
- Group
- Mathematical Informatics Group
- Title
- Associate Professor
- Degree
- Dr. of Science
- Research Field
- Class number / L-function / q-analogue

Current Research
Theory of Cyclotomic Fields and Bernoulli Numbers
One vital concept in number theory is class numbers. It is no exaggeration to say that algebraic number theory started when it was noticed that a class number did not necessarily equal 1. The value of a class number cannot be estimated, although an explicit representation of a class number was given by Dirichlet's analytic class number formula for abelian fields. Moreover, there is only one theory that turns out the behavior and divisibility of class numbers : Iwasawa theory's of cyclotomic fields. The theory, which has been developed and is now generalized, greatly contributed to the recent resolution of Fermat's conjecture. However, a big barrier must be overcome if we expect further developments of number theory : Bernoulli numbers. In 1850 the proof of Kummer's criterion for Bernoulli numbers made a dazzling debut in number theory : "Fermat's conjecture is true for regular primes."We do admit that Kummer's criterion has faded somewhat because Fermat's conjecture has now been proved by A. Wiles. However, Fermat' conjecture does not give important information to Bernoulli numbers. The resolution of Fermat's conjecture need not diminish the importance of Bernoulli numbers because they are fascinating numbers that appear in the criterion for many important mathematical concepts. Number theory cannot be completed without conquering Bernoulli numbers. A technique called q-analogue is one approach to Bernoulli numbers. In q-analogue, we treat [1]=1, [2]=1+q, and [3]=1+q+q2…, which is defined by variable q, instead of ordinary 1, 2, and 3…. (Note that if q→1, we get ordinary numbers.) These numbers are closely related to ordinary numbers, and a lot of formulas with respect to these numbers have been proved. Numbers called q-Bernoulli numbers for ordinary Bernoulli numbers have also been defined, and many q-formulas have been proved. One reason to treat such numbers is that it is easier to discover or prove q-formula than an ordinary formula.
However, the objects of number theory, for which q-analogue is defined, are very few, and an important example suggesting a significant q-analogue for number theory cannot be found. For the above reasons, it is important that more objects systematically define q-analogue, and it is crucial to find the one with the true meaning from among them. We composed q-analogue by a quite new method in [2] (1992). We systematically defined q-analogue by this composition method, although we had to define it individually. Recently, this composition method turned out to be deeply related to formal group. That is, this composition method tied ordinary objects to quantum objects in a more natural shape. We want to advance the theory of q-analogue by using formal group. Finally, we aim to discover new formulas of Bernoulli numbers. The theory of q-analogue in number theory was founded by L. Carlitz in the late 1940's. We proved that a q-analogue could be defined in a certain kind of power series and discovered many new q-analogue formulas. Our theory put the base on q-Bernoulli and q-Euler numbers that were defined by L. Carlitz, and we defined an isomorhism (q-operator) from ordinary to quantum objects. We defined q-analogue as the image of the q-operator, discovered a new formula by isomorhic property of the q-operator, and gave another proof of formula for q-Bernoulli and q-Euler numbers. In addition, we proved that the composition method of q-analogue had the necessity by using formal group.
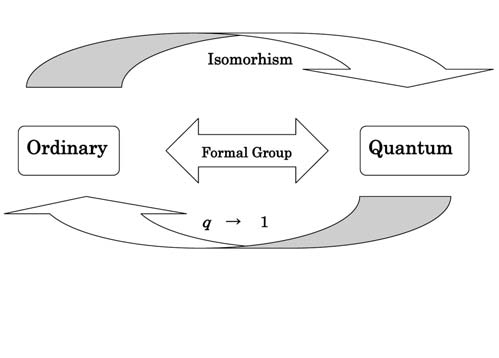
Figure : Formal group as a go-between for ordinary and quantam
Career
- 2003年 Associate professor of Graduate School of Information Science, Nagoya University
Academic Societies
- Mathematial Society of Japan
Publications
- q-Analogue of Riemann's zeta-function and q-Euler numbers, Journal of Number Theory 31 (1989), 346-362
- A construction of q-analogue of Dedekind sums, Nagoya Mathematical Journal 127 (1992), 129-143








