研究者総覧「情報知」
計算機数理科学専攻
- 氏 名
- 草刈 圭一朗(くさかり けいいちろう)
- 講座等
- 計算論講座
- 職 名
- 准教授
- 学 位
- 博士(情報科学)
- 研究分野
- 定理自動証明 / プログラム検証 / 計算モデル

研究内容
プログラム自動検証
近年の計算機の発展には目覚ましいものがあり、人間には到底行えないような計算も簡単に行えるようになってきている。一方、計算機は、少し数学的素養がある人なら簡単に行えるような証明すら行うことができない。これは、証明なるものを実行するには、単純な計算力だけではなく、なんらかの感性が要求されるためである。定理自動証明の研究とは、計算と証明の間を繋ぐ架け橋を学ぶことである。また、特に興味深い応用として、プログラム自動検証法の研究に取り組んでいる。この応用が可能なのは、プログラムを検証する際に必要となる様々な概念が、ある種の数学的な定理として定式化できるからである。以下では研究テーマごとに紹介していく。1. 計算モデル
私が興味を持っている関数型プログラミング言語では、関数を引数や値として取り扱える高階関数の導入により、高いレベルの抽象化を実現し言語の表現力を高めている。しかしながら、関数型プログラミング言語の計算モデルとして盛んに研究されている項書換え系は高階関数を直接取り扱えない。そのため、蓄積された豊かな理論的成果をプログラム自動検証へ応用することが困難である。よって、高階関数を直接取り扱える高階書き換え系の研究が近年盛んに行われている。しかし、高階書換え系の研究は理論的興味が優先されてきたため、関数型プログラミング言語のモデルとして見た場合には、不必要と思われる高度な表現力を持つ定式化が行われてきた。この反省にもとづき我々は、理論的に取り扱いやすいように制限しながらも高階関数を直接取り扱える計算モデルである単純型項書換え系を提案した。単純型項書換え系は従来の項書換え系と親和性が高いため既存の成果が利用しやすく、さらに関数型プログラミング言語との親和性も高いため、より実用的な成果が期待できる。現在は、関数型プログラミング言語において広く取り扱われていながらも単純型項書換え系では直接表現できない様々な概念(文脈依存性、規則の優先順位、レコード型など)を単純型項書換え系に組込んだ計算モデルの設計と、その解析に取り組んでいる。
2. プログラム停止性証明
停止性を持つプログラムは、それ自体が重要であるのみならず、評価の簡約関係自体を帰納法の土台として利用できるため、帰納法に基づく定理自動証明法への貢献が大きい。プログラム理論における代表的な停止性証明法としては、Taitによって導入された強計算性の概念に基づく手法、Dershowitzによって導入された単純化順序の概念に基づく手法、そしてArtsとGieslによって導入された依存対法が知られている。我々はこれらのうち強計算性の概念と依存対法を組み合わせることに成功した。現在、依存対法を適用するとき必要となる様々な手法(引数切り落とし法、依存グラフ解析法など)の研究に取り組んでいる。
3. 暗黙帰納法と高階完備化手続き
プログラム中で利用されるデータ構造の多くはリスト構造や木構造のように帰納的な構造を持っているため、プログラムが保証すべき性質の多くは帰納法を用いないと検証することができない。よって、計算機上での実行が容易である潜在帰納法や書き換え帰納法と呼ばれる暗黙帰納法の研究が盛んに行われてきた。暗黙帰納法は完備化手続きと呼ばれる手続きを用いると容易に実現することができる。我々は、暗黙帰納法の本質的な原理が単純型項書換え系上でも成立することを示し、さらに、完備化手続きを単純型項書換え上で定式化し実装を行い様々な解析を行っている。現在、これらの成果に基づくプログラム自動検証システムの構築に取り組んでいる。
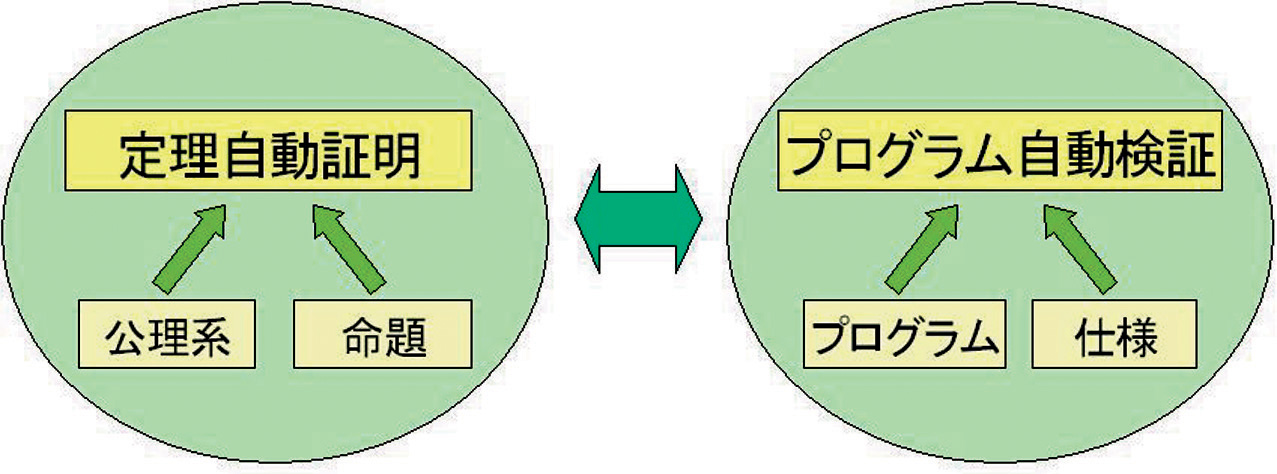
定理自動証明とプログラム自動検証
経歴
- 2000年北陸先端科学技術大学院大学情報科学研究科博士後期課程修了、博士(情報科学)
- 2000年東北大学電気通信研究所助手
- 2003年名古屋大学大学院情報科学研究科情報システム学専攻講師
所属学会
- 日本ソフトウェア科学会
- 電子情報通信学会
- 情報処理学会
主要論文・著書
- Kusakari,K., Sakai,M., Static Dependency Pair Method for Simply-Typed Term Rewriting and Related Techniques, IEICE Transactions on Information and Systems, Vol.E92-D, No.2, pp.235-247, 2009.
- Kusakari,K., Sakai,M., Enhancing Dependency Pair Method using Strong Computability in Simply-Typed Term Rewriting, Applicable Algebra in Engineering, Communication and Computing, Vol.18, No.5, pp.407-431, 2007.
- Kusakari,K., Nakamura,M., Toyama,Y., Elimination Transformations for Associative-Commutative Rewriting Systems, Journal of Automated Reasoning, Vol.37, No.3, pp.205-229, 2006.











