研究者総覧「情報知」
計算機数理科学専攻
- 氏 名
- 安本 雅洋(やすもと まさひろ)
- 講座等
- 情報数理基礎論講座
- 職 名
- 教授
- 学 位
- 理学博士
- 研究分野
- 数理論理学 / 超準モデル / 多項式時間計算量

研究内容
超準モデルとその計算量理論への応用
超準モデルの応用は、1960年代にA. Robinsonによる解析学への応用(超準解析)が最初で、無限小の概念の合理的な使用によってε-δ論法なしで解析学の基礎付けが可能であることを示した。その後1970年代にはA. RobinsonとP. Roquetteは整数環及び有理数体の超準モデルとそれらの有限次代数拡大体に埋め込まれる関数体の構造との関係、特に両者のdivisorが比例するとともにある種のdivisorの次数の限界がRothの不等式を使って表されることを示し、その結果を不定方程式論をはじめとする整数論、特に代数曲線上の整数点に関するSiegelの定理の証明やHilbertの既約性定理の研究などに使った。iteratedな超準モデルの使用などこれらの方法をさらに発展させることにより、ヒルベルトの既約性定理が成立する範囲の限界の決定等において従来の代数的手法では得られない結果が得られる。特に代数体と代数関数体の類似性が超準モデルの手法を使って表現することによって、よりいっそう明確になり、それらの応用可能性は代数曲面の整数点の分布の研究にもつながっている。超準解析においては飽和モデルをはじめとして非常に強い超準モデルが使用されているのに対して、1980年代半ばから弱い算術、特に限定算術の超準モデルの研究がさかんになりつつある。限定算術はS. Bussによって始められたもので、多項式時間計算量の理論の数学的基礎理論として重要なものである。この弱い算術の超準モデルにより、大きい数(2進表示された数)と小さい数(桁数として使用される数、i. e. 2進表示された数のbitの長さ)の区別が明確になる。通常の自然数で考えている限りこの両者は概念としては区別されても、数としては区別されないものであったが、超準モデルの使用により両者は区別可能となり、小さい数を保存したまま大きい数を拡大するといった方法が開発されるようになった。このことを使い最初に意味のある結果を得たのはAjtaiで、弱い算術の超準モデル上にforcing methodを応用することによってPHP(Pigeon hole principle)が多項式sizeで深さ有限のBoolean formulaでは書けないことを示した。この方法を限定算術の超準モデルのBool値拡大の理論に一般化することにより、弱い算術においては数え上げ(Counting)がPHPより強い条件であることが証明できる。またBool代数を多項式sizeのBoolean circuitを含むように拡大することによって、多項式時間計算量の階層の分離問題、特に計算量理論の中で最も重要な未解決問題と言われているP=NP問題との関係に関する研究に役立てることが可能になった。さらにオラクル部分のBool拡大への発展が考えられるが今のところ有効な理論はできていない。このようにして計算量理論の問題が超準モデルのBool代数のイデアルの完全性の構造の問題として取り扱えることがわかり、新しい視点からP=NP問題に取り組むことができるBool値拡大の方法は公理的集合論において数多くの優れた結果を生み出しており、同様のことが計算量の理論においても可能であると考えられる。
弱い限定算術の超準モデルの延長拡大の構造が、PとNPやPSPACEとの分離問題と関係が深いことがわかってきている。Bool拡大が横(巾)への拡大とすると延長拡大は縦(長さ)への拡大と考えることができる。P=NPやP=PSPACEなどを仮定すると、この縦への拡大が種々の良い性質を持つことが示される。一方ある種の延長拡大は対角線論法に類似の手法により不可能であることが示される。延長拡大の構成には1階限定算術の超準モデルの有界オラクルの定義可能性と帰納法との整合性が密接に関係している。この二つの手法をうまく融合させることによって計算量の分離問題の研究に役立てることができると期待される。
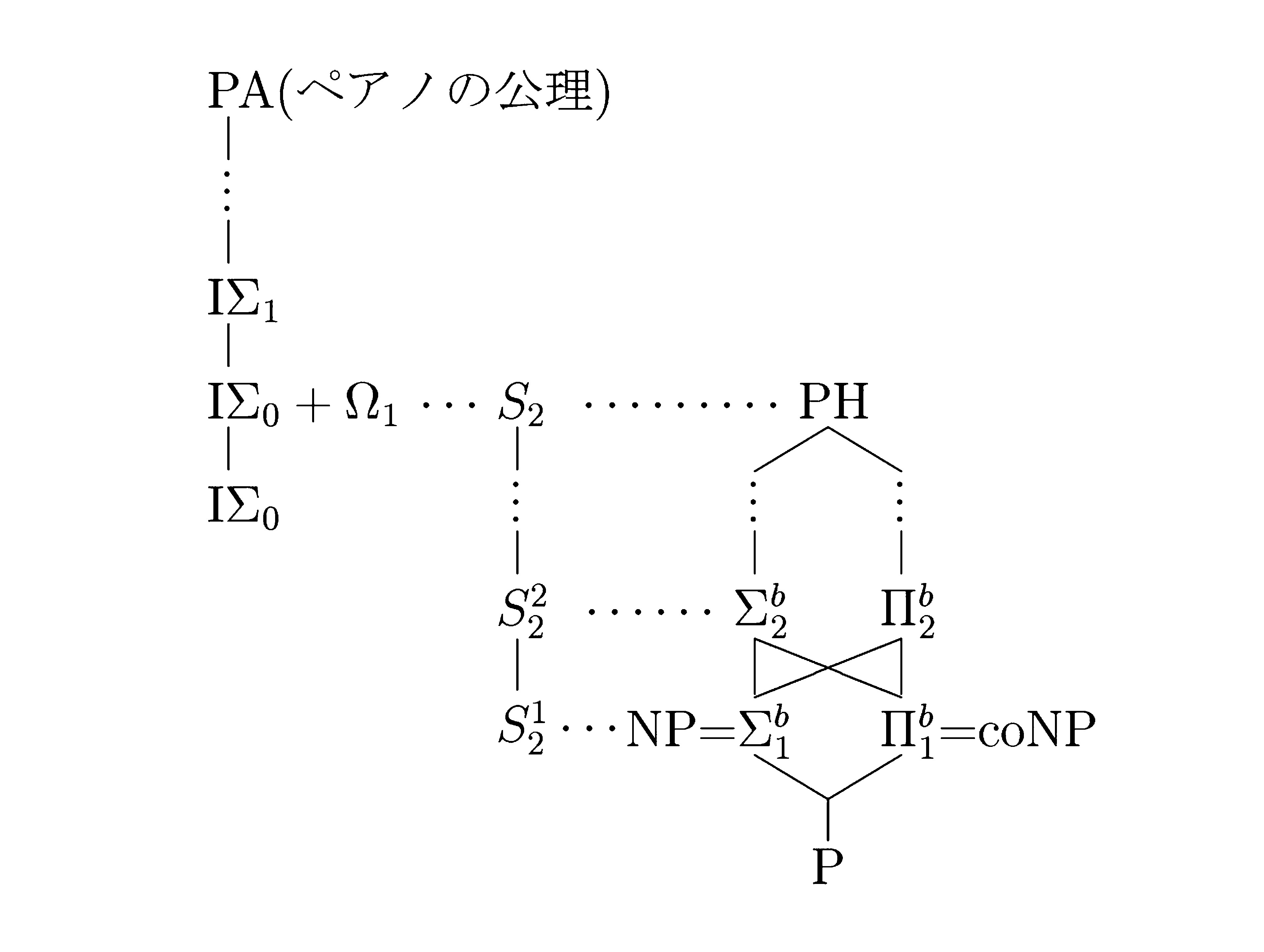
自然数論と多項式時間計算量の階層
経歴
- 1981年 名古屋大学大学院理学研究科博士課程後期課程修了
- 1981年 名古屋大学理学部助手
- 1987年 名古屋大学教養部講師
- 1993年 名古屋大学理学部助教授
- 1999年 名古屋大学人間情報学研究科教授
所属学会
- 日本数学会
- Association for Symbolic Logic
主要論文・著書
- Separation of first and second order theories i bounded arithmetic, Archive for Mathematical Logic 44 (2005) 685-688.
- Forcing on bounded arithmetic II, Journal of Symbolic Logic 63 (1998) 860-868.
- Nonstandard arithmetic and Hibert subsets, Annals of Pure and Applied Logic 52 (1991) 195-202.











