研究者総覧「情報知」
計算機数理科学専攻
- 氏 名
- 神保 雅一(じんぼう まさかず)
- 講座等
- 情報数理基礎論講座
- 職 名
- 教授
- 学 位
- 理学博士
- 研究分野
- 離散数学 / 統計学 / 離散数学の情報通信などへの応用

研究内容
離散数学とその統計的データ解析、情報通信への応用
■研究の概要■離散数学から統計学の領域を研究対象としている。特に、組合せデザイン、グラフなどの組合せ構造を、離散データ解析、情報通信における符号・暗号の理論、DNA解析のためのpooling designや識別アルゴリズムなどに適用する際に、組合せ構造の差異に起因する効率の差、最適性の問題に焦点を当てて、その組合せ論的研究および応用の研究を行っている。
■研究テーマ■
(1) 組合せデザインとその応用に関する研究
統計的実験計画法では組合せ配置の研究が重要であり、古くから組合せデザインと呼ばれる組合せ構造の最適性および構成法などの研究がなされてきた。例えば、4つの物の重さを天秤ばかりで測定する際に、これらの4つをひとつずつ順に測定してその重さを測る方法もあれば、まず、3つを一方に乗せ、残りのひとつを他方に乗せて、その重さの差を測り、次に、異なった組合せで3つの組と一つに分けてその差を測ることを合計4回繰り返し、その結果から個々のものの重さを推定する方法もある。いろいろな方法が考えられるが、この問題には、アダマール行列などの組合せデザインが深く関与している。組合せデザインは符号理論とも密接な関係があり、CDMA(Code Division Multiple Access)と呼ばれる携帯電話などの通信方式にもアダマール行列が用いられている。また、暗号の理論もこの20年ほど離散数学の研究分野として研究がなされて来たが、そこには、整数論、有限体上の楕円曲線、有限幾何、直交配列、組合せデザインなど種々の組合せ論を含む代数的理論が用いられている。暗号の理論は現在では、Internet上でのセキュリティを保証する基礎的技術である。
当研究室では、これらの問題に生じる組合せ構造に焦点を当てて、その組合せ論的特徴、最適性、構成法などの研究を行っている。
(2) DNA library screenigのためのpooling designの組合せ構造およびpositive識別アルゴリズムの研究
DNA library screeningでは、数万におよぶ多数の塩基列(A、T、C、Gの列)の中から、ある試験に対して陽性(positive)反応を示す塩基列を見出す試験がよく行なわれる。このテストの際に、v個の各塩基列を一つ一つテストするとv回のテストが必要になるが、複数の塩基列をひとつにまとめてそのグループ(poolと呼ばれる)に対して、反応試験を行なうと、そのプールが陰性(negative)であった場合には、プール内の塩基列はすべて陰性であることを1回のテストで判定できる。このように実験回数を削減する方法をグループテストと呼んでいる。このようなさまざまな種類のpoolを作ってグループテスト(あるいはpooling experiment)と呼ばれる実験手法を用いることがある。グループテストでは、その効率を高めるために多くのクローンの中から出来るだけ少ないプール数で目的のクローンを見出すことができる実験を計画することが重要である。このためにクローンの集合からプールと呼ばれる部分集合の族をうまく選ぶ組合せ論的アプローチが有効である。また、このようなテストでは、実験結果にfalse positive、false negativeなどの誤りが生じることは避けられない。本研究室では、実験結果に誤りがある場合について、効率の良いpooling designの組合せ論的特徴を見出し、その構成法を与えることおよびpositiveな塩基列を見出すためのアルゴリズムの開発を行ない、ベイジアンネットワークを用いて各poolの実験結果からpositiveなcloneを見出すための効率的なアルゴリズムを開発した。また、従来のMCMC(Markov chain Monte Carlo)による判定アルゴリズムとの比較を行い、実用に供するための知見を得て、本アルゴリズムを用いた識別法で特許を取得した。
(3) 試験の成績などに関する統計的データ解析
アンケート調査、選択式試験などにおけるyes/noあるいは多枝選択などの離散データを解析することが必要になることが多々ある。企業活動、社会活動において生じるこのようなデータの解析には、その問題に即した統計手法を開発し、最適なデータ解析をすることが重要である。当研究室では、中学生の模擬試験の2値データから本人の基礎学力、理解度などを推測するデータ解析などのテーマにも取り組んでいる。
■今後の展開■
組合せ構造の数理的研究を進展させると共に、その統計的実験計画、情報通信、暗号、DNA解析などの分野への応用の研究を発展させて行きたい。
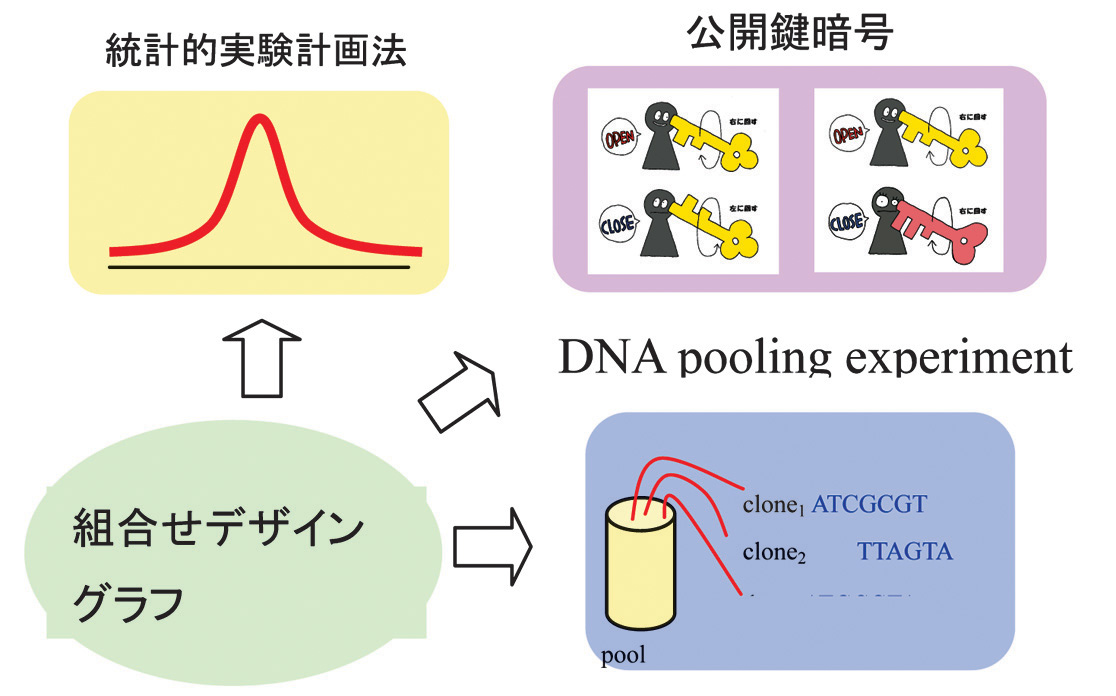
組合せ論から応用へ
経歴
- 1976年東京工業大学大学院理工学研究科情報科学専攻修士課程修了。理学博士。
- 1976年東京理科大学理工学部助手。
- その後、筑波大学社会工学系講師、岐阜大学工学部助教授・教授、慶應義塾大学理工学部教授を経て2004年名古屋大学情報科学研究科教授。現在に至る。
所属学会
- 日本数学会
- 日本統計学会
- 応用統計学会
- 情報処理学会
- 日本オペレーションズリサーチ学会
- ICA
- AMS
主要論文・著書
- M. Mueller and M. Jimbo, Consecutive positive detectable matrices and group testing for consecutive positives. Discrete Math. 279 (2004), 369-381.
- M. Mueller and M. Jimbo, Erasure-resilient codes from affine spaces. Discrete Appl. Math. 143 (2004), 292-297.
- K. Ozawa, M. Jimbo, S. Kageyama, S. Mejza, Optimality and constructions of incomplete split-block designs. J. Statist. Plann. Inference, 106 (2002), 135-157.











