Comprehensive List of Researchers "Information Knowledge"
Department of Complex Systems Science
- Name
- NAKAMURA, Yasuyuki
- Group
- Many-body Systems Science Group
- Title
- Associate Professor
- Degree
- Dr. of Engineering
- Research Field
- e-Learning / Statistical physics / Econophysics

Current Research
Theoretical and Simulation Approach to a Multi-Agent Game
OUTLINEThe theory and technique of statistical physics, originally developed to investigate condensed matter, have recently been applied to information sciences such as neural networks and image processing, and even to social sciences. By applying statistical physics, especially statistical physics of spin systems, and computer simulation, we are studying economic systems. To be more precise, we are investigating a Minority Game and its extension as a model of an economic system. The Minority Game proposed in 1997 is one of the simplest models that implements the principle of a minority mechanism, and it displays complex and rich behavior. Our current work involves extending the Minority Game, constructing a more realistic model of an economic system, and carry out computer simulations of the model. Furthermore, we are conducting a theoretical investigation of the Minority Game because of its simplicity.
TOPICS
(1) Effect of investment in a Minority Game
Income and wealth distribution of a higher-income group is known to obey a power law distribution (Pareto law). Whether or not that kind of distribution is also realized in a Minority Game, which reflects an aspect of social phenomena, the origins of the distribution are our interests and those are what we are investigating here. Our recent research revealed that a power law distribution is at work when agents of the game invest a given amount according to their wealth. Figure 1 shows a wealth distribution on a logarithmic axis. The horizontal axis denotes wealth and vertical axis is a cumulative distribution. We plan to take a theoretical approach to support this simulation result in the future.
(2) Artificial market model based on the Minority Game
It is very interesting that the Minority Game shows complex and rich behavior in spite of its simplicity, but the Minority Game itself is not a complete model of an artificial market. Therefore, there have been many extensions of the Minority Game to date, which relate to economic phenomena in the real world. Extended Minority Games are useful for pursuing answers to the following questions : What is the true nature of an artificial market, and what is required for modeling an artificial market ?
(3) Stochastic process of a Minority Game
Deriving the time evolution of macroscopic behaviour of a market from a microscopic model that describes agents' individual behavior is one popular approach to investigate a market model. Since the Minority Game is a microscopic model, deriving the time evolution of a macroscopic behavior is a powerful approach for investigating the origin of a power law distribution of wealth in a Minority Game extension.
EDUCATION
We are also interested in physics education in an undergraduate school. We are developing educational materials with use of symbolic computation software and constructing a computer system integrated with those educational materials with an eye to developing an e-Learning system.
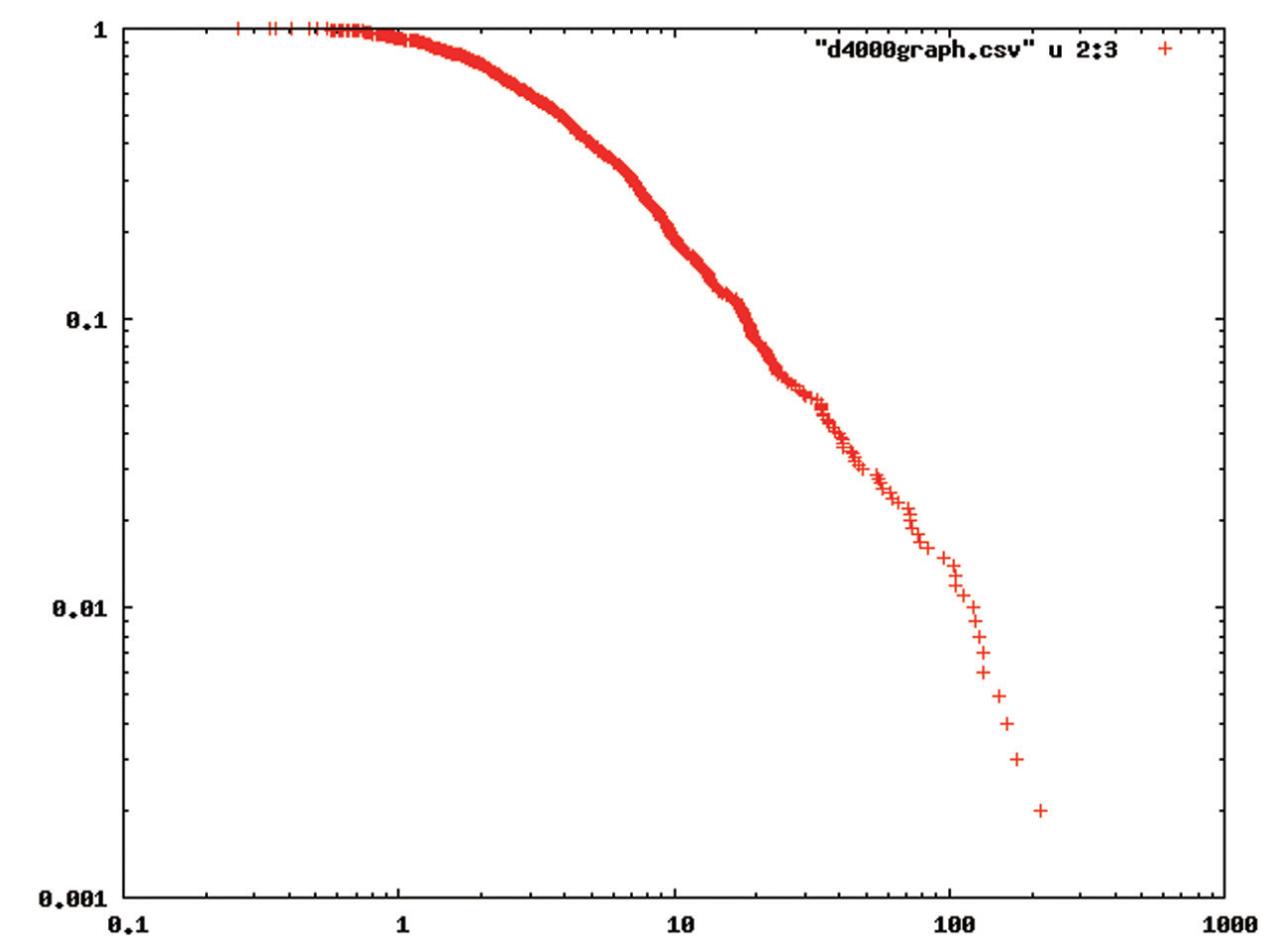
Figure : Power law distribution of wealth in a MG.
Career
- Yasuyuki Nakamura received his Dr. of Engineering degree in applied mathematics and physics from Kyoto University in 1995.
- He was a Research Assoc. from 1995 to 2004.
- Since 2004, he has been an Assoc. Prof. at the Graduate School of Information Science, Nagoya University.
Academic Societies
- JPS
- IPSJ
- JSSAC
- CIEC
- JSiSE
- JSAI
Publications
- The Dynamics of Wealth in the Minority Game, IPSJ TOM, vol. 147, pp. 138-143 (2006).
- A Fashion Model with Social Interaction, Physica, A 337, pp. 625-634 (2004).
- Monte Carlo Study of a Mixed Spin-1 and Spin-3/2 Using Ferromagnets, IEEE Transactions on Magnetics, 5, pp. 2406-2408 (2002).








