Comprehensive List of Researchers "Information Knowledge"
Department of Complex Systems Science
- Name
- SUGIYAMA, Yuki
- Group
- Many-body Systems Science Group
- Title
- Professor
- Degree
- Dr. of Science
- Research Field
- Field theories / Dynamical phase transition of manybody systems / Dynamics of self-driven particles

Current Research
Mathematical Physics on Dynamics of Many-body Systems
OUTLINEAny phenomenon in natural and social sciences can be understood as a macroscopic aspect organized from the collective motion of microscopic elements. Our research aims seek to reveal the general mathematical structures in complex phenomena in the nonlinear and nonequilibrium dynamics of such many-body systems. The research fields cover such material objects as elementary particles, spin systems, and granular media, and such social objects as traffic flow, pedestrians, collective bio-motions, and networks. Methods include mathematical analysis such as field theories, renormalization group, difference-differential equations, dynamical systems, and quantum physics as well as computer simulations.
TOPICS
(1) Field Theories and Renormalization Group
Field theories explain high energy physics and the evolution of the universe. Analysis methods are related to statistical physics and dynamical systems. We study gauge theories and spin systems using renormalization group methods. The periodic points of complex valued RG equations imply the universality of the mathematical structure of field theories. Such a viewpoint provides a new spectroscope of systematic understanding and classification for phase transition phenomena and field theories in the systems of infinite degrees of freedom.
(2) Mathematical Modeling Traffic Flow
Traffic flow can be deeply understood as a many-body physical system, and the formation of a traffic jam is a collective phenomena of interacting particles (vehicles), such as phase transition and pattern formation. We introduced a mathematical model called Optimal Velocity Model (OVM) of a nonlinear dynamical system that reproduces a spontaneous traffic jam formation as a traveling cluster solution of a system of dissipative equations. OVM is widely established as the basic mathematical model for traffic flow and is analyzed from several mathematical and physical aspects. The jamming transition indicates subcritical Hopf bifurcation, which implies a strong relation to biophysical systems.
(3) Cluster in Dissipative Systems and Solitons
OVM is the simplest model of a nonequilibrium physical system and causes the emergence of moving clusters as a dynamical phase transition, which is controlled by parameters. Dissipative systems in the OVM-class are exactly solvable, and traveling cluster solutions are described by elliptic functions. The model is strongly related to integrable soliton systems that provide a mathematical aspect of the mechanism of complex systems.
(4) Dynamics of Self-Driven Particles
Self-driven (SD) particles organize a dissipative system with asymmetric interaction, which produces a remarkable difference from an energy conserved system with symmetric interaction for ordinal physics for materials. The simplest example is a traffic flow, OVM. The dynamics of SD particles is a new branch of physics that can express many phenomena of complex systems, such as nonequilibrium material systems, biological systems, and social systems. It can also provide a unified view on the physical mechanisms of several complex phenomena.
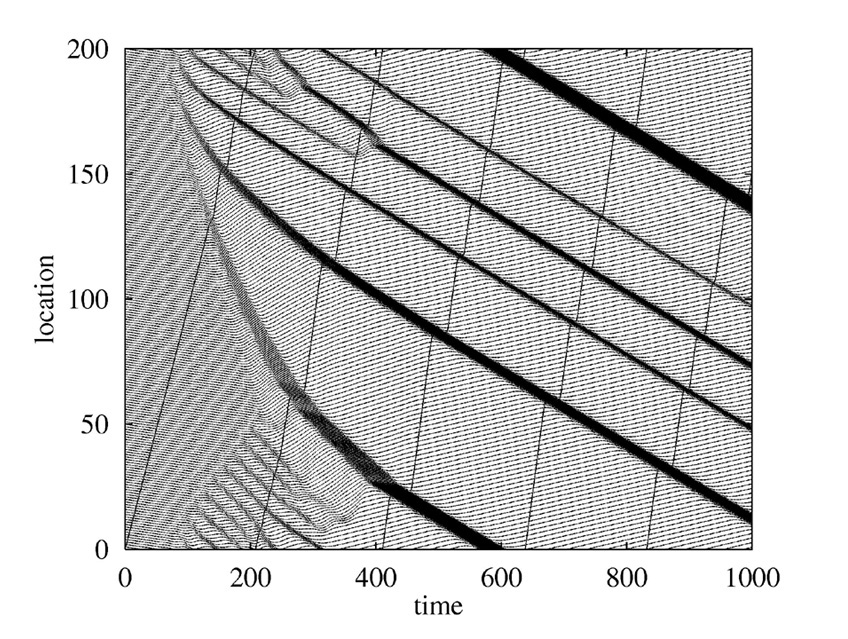
Figure : Forming a cluster (a traffic jam) in OVM
Career
- Department of Physics, Graduate School of Science in Nagoya University, Doctor of Science (1985).
- Research Associate at Nagoya University (1988).
- Associate Professor at City College of Mie (1990).
- Research Fellow of the Institute of Theoretical Physics in Bern University (1994).
- Associate Professor at Nagoya University (2002).
- Since 2004, Professor at Nagoya University.
Academic Societies
- Physical Society of Japan
- Japan Society for Industrial and Applied Mathematics.
Publications
- The Renormalization Group Study of the Effective Theory of Lattice QED, Physics Letters, B223, 445-450 (1989).
- Dynamical Model of Traffic Congestion and Numerical Simulation, Physical Review, E 51 (1995) 1035-1042.
- Traffic and Granular Flow '01 (Springer-Verlag) (2003).








