Comprehensive List of Researchers "Information Knowledge"
Department of Computer Science and Mathematical Informatics
- Name
- YOSHINOBU, Yasuo
- Group
- Mathematical Informatics Group
- Title
- Professor
- Degree
- Dr. of Philosophy
- Research Field
- Mathematical logic / Axiomatic set theory

Current Research
Infinitary Combinatorics and Large Cardinal Axioms
My research area is mathematical logic, or more specifically, axiomatic set theory. My main interest is in a series of axioms called Large Cardinal Axioms and infinitary combinatorics relevant to those axioms.(1) Background : What is a Large Cardinal ?
At the end of the 19th century, Cantor discovered that there is no one-to-one correspondence between N (the set of natural numbers) and R (the set of real numbers), which means that there are distinct levels in the size of infinite sets (cardinalities).
Concerning the first significant problem, Cantor conjectured that no other cardinalities exist between those of N and R (The Continuum Hypothesis : CH), but he couldn't prove it. Later, to solve such problems, an axiom system of set theory called ZFC was established by Zermelo and Fraenkel that consistently argued their intuition on the nature of infinite sets.
However, Gödel and Cohen later showed that, from ZFC alone, CH cannot be determined either true or false.
One possible solution to such problems is to add some natural, persuasive axioms to ZFC.
Gödel conjectured that, assuming the existence of a large set with some strong properties (large cardinal axioms), one can determine various independent propositions such as CH.
Although this conjecture turned out false when taken literally, his idea was succeeded by later researchers, and it has been discovered that many propositions about the properties of the sets of real numbers (Lebesgue measurability, the Baire property, etc.) are decided by large cardinal axioms. Now the theory of large cardinal axioms has become one of the main research objects of modern set theory.
(2) What I study
I study the influences of large cardinal axioms or their variations called forcing axioms on the aspects of infinitary combinatorics around ω2. In relation to this, I look at the preservation of these axioms under forcing (a general technique developed by Cohen in his proof of the independence of CH to transform a model of set theory by extension) that have no influence on small cardinals. I have learned that, in this area, conclusions are sometimes delicate and interesting.
For instance, as a recent result of a joint work with Konig, although Martin's maximum (MM : a forcing axiom) can be destroyed by ω2-closed forcing, it is never destroyed by a directed ω2-closed (slightly stronger property than ω2-closure) forcing and that there are forcing axioms considerably closer to MM that can be preserved under any ω2-closed forcing.
I feel an odd coincidence in the fact that Namba forcing, introduced by Kanji Namba at Nagoya University more than 30 years ago, plays an essential role in the above results.
(3) Future prospects
As a long-term project, I am interested in the theory of inner models for large cardinals.
Another trait of large cardinal axioms is that they are mostly queue linearly in order of strength and play the role of a measure that measures the "consistency strength" of propositions : many well-known propositions in set theory have turned out equivalent to either of these axioms in the sense of consistency. Forcing and inner model theories are the main tools to measure propositions in this sense.
In contrast to forcing, which has been widespread as a standard technique among set theorists, the theory of inner models, which is only studied by a handful of researchers, suffers from a lack of basic documents. My long-range goal is to break this situation.
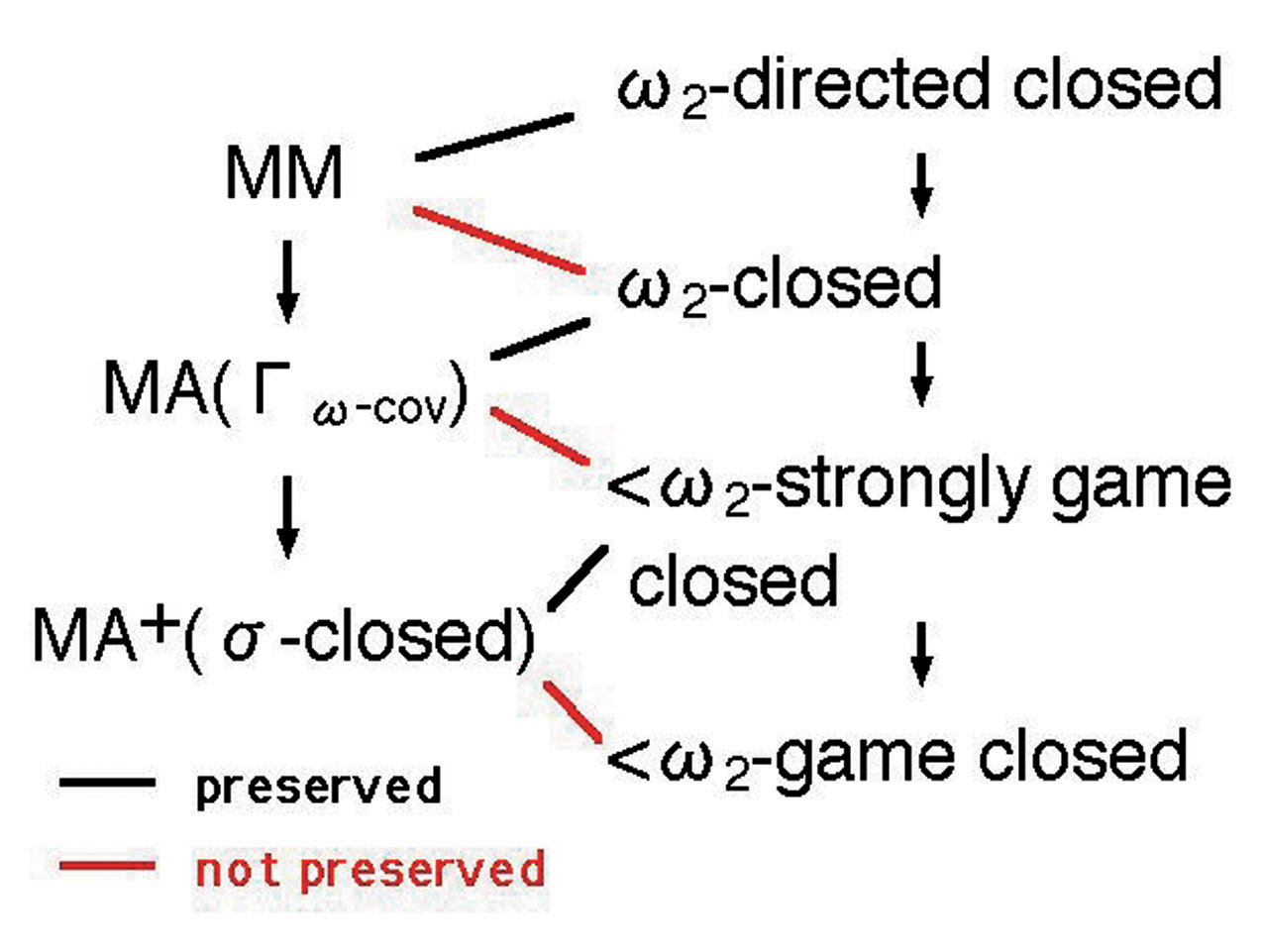
Figure : Forcing axioms vs. Classes of posets
Career
- 1994 Master of Sci., Grad. Sch. of Sci., Nagoya Univ.
- 1995 Left Ph. D. course of Grad. Sch. of Sci., Nagoya Univ.
- 1995 Research Associate, Grad. School of Human Informatics, Nagoya Univ.
- 2003 Research Associate, Graduate School of Information Science
- 2005 Current Position
- 1995-1996 Visiting researcher at Univ. of California, Los Angeles
- 2002-2003 Research scholar abroad aided by MEXT (Univ. of California, Irvine)
Academic Societies
- Math. Soc. of Japan
Publications
- How many miles to βω ? " Approximating βω by metricdependent compactifications (with Masaru Kada and Kazuo Tomoyasu) Topology and its Applications, 145 : 277-292, 2004.
- Fragments of Martin's Maximum in generic extensions (with Bernhard König) Mathematical Logic Quarterly, 50 (3) : 296-302, 2004.
- Approachability and games on posets, Journal of Symbolic Logic, 68 (2) : 589-606, 2003.








