 |
In the range of the Reynolds number and the aspect ratio considered in this paper, a pair of cells whose boundary has inward radial flow loses its power when the flow with N+2 cells changes into a flow with N cells during or after the reduction of the rotation speed of the inner cylinder. In the transition from flow with an anomalous cell, the extra cells developing on an end wall merge and a new single cell swirling in the normal direction is formed. Then, the new cell grows and a pair of cells adjacent to the new cell disappears. The pair of weakening cells has a boundary between them with inward radial flow.
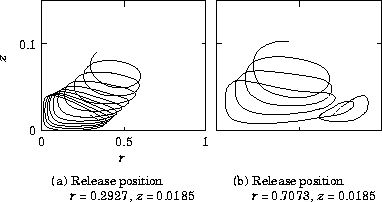
The anomalous cell, which is originally attached to the end wall, is detached from the wall by the development of extra cells. As confirmation of this, the path lines of passive particles which are initially captured by extra cells are shown in Fig. 11. The outer extra cell extends in the radial direction and covers the inner extra cell, and then a merged single cell is formed.
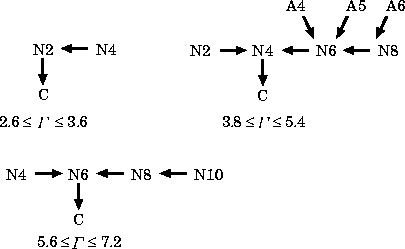
Figure 12 shows partial order structures representing transition processes to primary modes with 2 cells, 4 cells and 6 cells, which are confirmed by the present calculation. While a greater number of transitions were found in experiments (Nakamura et al., 1989), the structures shown in Fig. 12 are not inconsistent with experimental results. Since there may not be any rational reasons why the correspondences between computational prediction and experimental results are not complete, it cannot be denied that the precision of the calculation is not sufficient enough or that the observed transitions result from some tolerances associated with the fabrication of the experimental apparatus.
Bolstad and Keller (1987) argued that an anomalous mode contains a hidden vortex between the anomalous cell and the end wall of cylinders, though an anomalous cell appears to cause outward flow near the end wall. The existence of an anomalous cell and extra cells in Fig. 6 and the profile of the strain rate in Fig. 7 show that there is a region between extra cells, where the anomalous cell reaches the end wall. That is, while the extra cells accelerate inward flow, the anomalous cell has outward flow. This result has been confirmed experimentally (Nakamura and Toya, 1996), and it is different from the one reported by Bolstad and Keller.
 |
 |
The flow with an anomalous cell(s) has more mean kinetic energy than the flow with the primary mode. The anomalous mode may have some mechanism which efficiently transfers the energy supplied by the inner cylinder to the region near the fixed end walls.
When the Reynolds number exceeds a certain value, Taylor vortex flow forms azimuthal waves. For a relatively small aspect ratio at which the 2-cell or 4-cell mode appears, Mullin and Benjamin (1980) presented the critical Reynolds number for the onset of time-dependent motion. Their result shows that the value is almost higher than 750 in the case of the radial ratio 0.615. In the present study, the Reynolds number is 700 at most, and it can be said based on the experimental finding that the Taylor vortex flows shown above are not wavy flows.