Transformation from normal mode

**Figure 1:** Bifurcation from secondary normal mode to primary mode.
$\begin{figure} \epsfile{file=material/cell-formation/cell-formation.eps,scale=1.0} \end{figure}$

**Figure:** Development of flow field from secondary normal mode to primary mode. The aspect ratio is 4.6 and the Reynolds number is reduced from 150 to 140. Deceleration starts at t = 450 and it ends at t = 900
$\begin{figure} \epsfile{file=material/sympo/fig03.eps,scale=1.0} \end{figure}$

As found in the previous work, the primary mode appears at a low Reynolds number, and secondary mode is established when the Reynolds number is higher (Benjamin, 1979; Nakamura et al., 1989). The number of cells (N) of the primary mode is uniquely determined by the aspect ratio. Suppose that secondary mode with N+2 cells is found at a certain Reynolds number Re₁, and primary mode with N cells appears when the Reynolds number is reduced from Re₁ to Re₂. 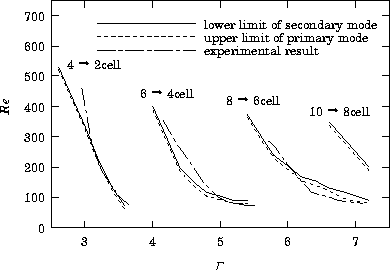The ranges of the Reynolds number in which the mode exchange occurs are shown in Fig. 1, where the difference between two Reynolds numbers Re₁ and Re₂ is narrowed to about 10 and the deceleration is slowed. The results of the quasi-steady experiment are also presented in the figure. The transitions from the 4-cell to the 2-cell mode at $2.8 \leq {\sl\Gamma} \leq 3.6$ , from the 6-cell to the 4-cell mode at $4.0 \leq {\sl\Gamma} \leq 5.4$ and from the 8-cell to the 6-cell mode at $5.4 \leq {\sl\Gamma} \leq 7.2$ are predicted, and they show good qualitative agreement with the experimental results. The transition from the 10-cell to the 8-cell mode at $6.6 \leq {\sl\Gamma} \leq 7.4$ is not confirmed by the experiment.

The critical Reynolds number at which the Taylor vortex flow develops in an infinite annulus with the same radius ratio as in the present study is estimated to be about 45 (Koschmieder, 1993). Considering that the critical Reynolds number is almost independent of the aspect ratio (Cole, 1976), we can expect a well-developed Taylor vortex flow at a Reynolds number just above the critical value. For Re = 50, the primary mode appears throughout the whole range of aspect ratios covered in the present study. The result coincides with the experimental observation: 2 cells at $2.6 \leq {\sl\Gamma} \leq 3.6$ , 4 cells at $3.8 \leq {\sl\Gamma} \leq 5.4$ and 6 cells at $5.6 \leq {\sl\Gamma} \leq 7.2$ .

**Figure:** Variation of circumferential rate of strain on cylinder walls. The aspect ratio is 4.6 and the Reynolds number is reduced from 150 to 140. Deceleration starts at t = 450 and it ends at t = 900.
$\begin{figure} ~~~~~~\epsfile{file=material/sympo/fig04.eps,scale=0.9} \end{figure}$

**Figure:** Development of flow field from secondary normal mode to primary mode. The aspect ratio is 6.0 and the Reynolds number is reduced from 207 to 200. Deceleration starts at t = 621 and it ends at t = 1242.
$\begin{figure} \begin{center} \epsfile{file=material/sympo/fig05.eps,scale=0.9} \end{center}\end{figure}$

**Figure:** Development of flow field from secondary anomalous mode to primary mode. The aspect ratio is 5.4 and the Reynolds number is reduced from 700 to 80. Deceleration starts at t = 2100 and it ends at t = 4200.
$\begin{figure} \begin{center} \epsfile{file=material/sympo/fig07-upper.eps,scale... ...epsfile{file=material/sympo/fig07-lower.eps,scale=0.95} \end{center}\end{figure}$

**Figure:** Velocity vectors and contours of stream function ${\sl\psi }$ near the end wall with anomalous cell. The aspect ratio is 5.4 and the Reynolds number is reduced from 700 to 80. Deceleration starts at t= 2100 and it ends at t = 4200.
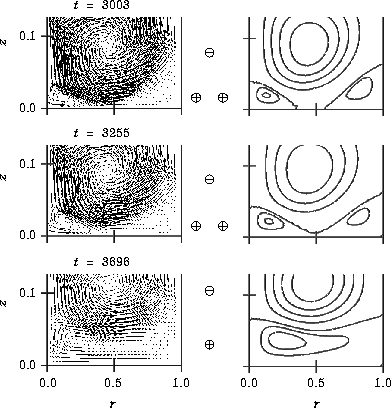$\begin{figure} \epsfile{file=material/sympo/fig08.eps,scale=1.0} \end{figure}$

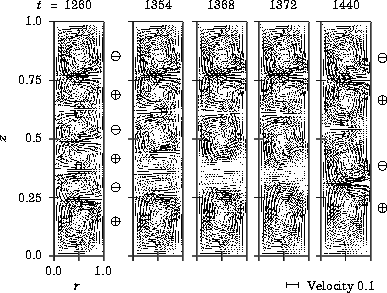
The variation of the velocity vectors in the (r, z) plane during the transition process from the normal secondary 6-cell mode to the primary 4-cell mode is shown in Fig. 2, with the inner cylinder at the left. The aspect ratio is 4.6, and the fully developed flow with Re = 150 is linearly decelerated to a flow with Re = 140. The velocity fields at t = 1260 and t = 1440 are accompanied by the plus symbol (+) which indicates that the swirling direction of a cell is clockwise and the minus symbol (-) which indicates the swirling direction is counterclockwise. Mode transition occurs after the deceleration ends at t = 900 and the Reynolds number becomes constant once again. First, a pair of counter-rotating cells, which is around the axial position z = 0.35, gradually weakens. The flow at the boundary between the two cells is inward, that is, the slower fluid convects towards the inner cylinder. Then, the pair of cells is overlapped by adjacent cells and disappears. As can be seen from this example, the transition phenomenon from a secondary mode with an even number of cells to another mode is not symmetric with respect to the midplane.

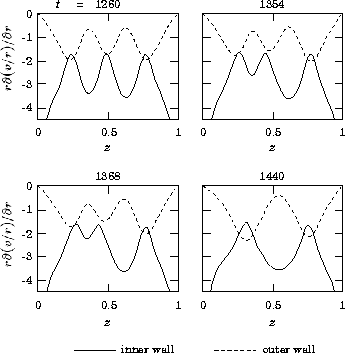
Figure 3 shows the variation of the circumferential rate of strain on cylinder walls during the mode transition shown in Fig. 2. As the transition proceeds, the absolute value on the inner cylinder wall decreases at about z = 0.35 where there exits a boundary of disappearing cells, and the radial inward flow is observed. The absolute value of the extremum on the outer cylinder, on the other hand, becomes smaller around the midplane where the radial flow is outward. After the extrema disappear, the flow mode changes to the primary 4-cell mode.

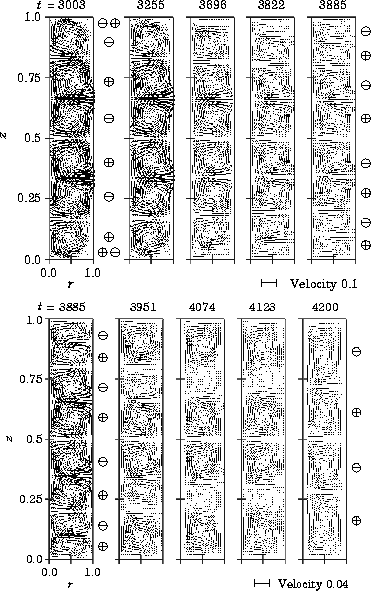
The variation of velocity vectors from a secondary 8-cell mode to a primary 6-cell mode is shown in Fig. 4, where the aspect ratio is 6.0 and the Reynolds number decreases from 207 to 200. The flow in the 8-cell mode is inward radial around the midplane, and a pair of cells is collapsed by adjacent cells.