Steady mode of fully developed flow

We examine fully developed flow modes at ${\sl\Gamma }$ from 0.1 to 1.6 with an interval of 0.1 and Refrom 100 to 1500 with an interval of 100. The Reynolds number Re is suddenly increased from zero to Re₀. At ${\sl\Gamma }$ more than unity, our experimental results show that the wavy Taylor vortex flow appears when Re₀ is more than about 1000. Therefore, the numerical results based on the axisymmetric equations may not be probable. On the other hand, when ${\sl\Gamma }$ is less than unity, the Taylor vortex flow is not in the ``wavy'' mode but in the ``rotation'' mode shown in Fig $% latex2html id marker 313 $.\,\,\ref{fig:table}$$ .

Figure 1 shows established mode patterns. Figures 2, 3 and 4 show velocity vectors in the normal two-cell mode (N2), anomalous one-cell mode (A1) and twin-cell mode (TWIN), respectively. In each velocity vector figure, the rotating inner cylinder is on the left and the stationary outer cylinder is on the right. Figures 3 and 4 include flow patterns obtained by Nakamura and Toya (1996).

When Re is small, the N2 mode is formed, as shown in Fig $% latex2html id marker 317 $.\,\,\ref{fig:two-cell}$$ . The N2 mode gives inward flow near the end walls and outward flow near the mid plane in the axial direction. This numerical evidence is confirmed by our experiment. In the N2 mode, symmetric and asymmetric patterns appear. In order to compare the symmetry about the mid plane in the axial direction, the coordinates of the maximum value of ${\sl\psi}$ , (r_max, z_max), and that of the minimum value of ${\sl\psi}$ , (r_min, z_min), are determined. While (r_max, z_max)=(0.46, 0.31) and (r_min, z_min)=(0.46, 0.69) in Fig $% latex2html id marker 331 $.\,\,\ref{fig:two-cell}$$ (a), (r_max, z_max)=(0.21, 0.17) and (r_min, z_min)=(0.42, 0.56) in Fig $% latex2html id marker 337 $.\,\,\ref{fig:two-cell}$$ (b). Cliffe (1983) calls this asymmetric flow ``single-cell flow''.

**Figure 2:** Velocity vectors in normal two-cell mode.
$\begin{figure} \epsfile{file=material/asy-2/asy-2-nc-02.eps,scale=1.0} \end{figure}$

**Figure 3:** Anomalous one-cell mode.
$\begin{figure} \epsfile{file=material/1cell/1-nc-02.eps,scale=1.0} \end{figure}$

**Figure 4:** Twin-cell mode.
$\begin{figure} \epsfile{file=material/twin/twin-nc-02.eps,scale=1.0} \end{figure}$

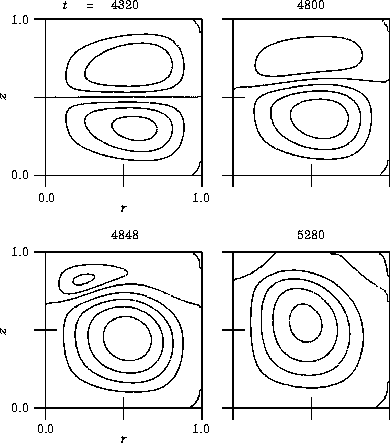
Figure 3 shows an example of the A1 mode. In Fig $% latex2html id marker 339 $.\,\,\ref{fig:one-cell}$$ (b), the anomalous cell rotates in a counterclockwise direction. It is accompanied by extra cells which rotate in the clockwise direction at both the inner and outer cylinder sides, though the extra outer cell is very weak and is not clearly shown. The calculated flow pattern agrees with the experimental result obtained by Nakamura and Toya (1996) shown in Fig $% latex2html id marker 341 $.\,\,\ref{fig:one-cell}$$ (a).

When ${\sl\Gamma }$ is from 0.6 to 0.9 and Re is from 1000 to 1500, the TWIN mode appears, as shown in Fig $% latex2html id marker 347 $.\,\,\ref{fig:twin-cell}$$ (b). The TWIN mode has separation points on both end walls of the cylinders. In Fig $% latex2html id marker 349 $.\,\,\ref{fig:twin-cell}$$ (b), two large cells and one small cell are observed. The large cell on the left rotates in a counterclockwise direction and the other large cell rotates in a clockwise direction. The small cell, which rotates in a clockwise direction, is located at the inner lower corner. Numerical results agree with the experimental results by Nakamura and Toya (1996) shown in Fig $% latex2html id marker 351 $.\,\,\ref{fig:twin-cell}$$ (a), although the corresponding Reynolds number is not exactly the same. As far as we know, numerical confirmation of the existence of the twin-cell mode is not given in the previous studies.

**Figure:** Time variation of mean enstrophy. ${\sl\Gamma }$ =0.5, Re=600.
$\begin{figure} \epsfile{file=material/enstrophy-graph/Re_600/forum/enstrophy.eps,scale=1.0} \end{figure}$

**Figure:** Time variation of mean enstrophy. ${\sl\Gamma }$ =0.5, Re=1500.
$\begin{figure} \epsfile{file=material/enstrophy-graph/Re_1500/enstrophy.eps,scale=1.0} \end{figure}$

**Figure:** Variation of streamlines at time points shown in Fig $% latex2html id marker 361 $.\,\,\ref{fig:ens-1500}$$ .
$\begin{figure} \epsfile{file=material/rotation-figure/rotation.eps,scale=1.0} \end{figure}$

**Figure:** Development of flow field from anomalous one-cell mode to normal two-cell mode. ${\sl\Gamma }$ is 0.8 and Re is reduced from 500 to 100. Deceleration starts at t = 900 and ends at t = 1800.
$\begin{figure} \epsfile{file=material/1-2/1-2-nc-01.eps,scale=1.0} \end{figure}$

**Figure:** Development of flow field from normal two-cell mode to anomalous one-cell mode. ${\sl\Gamma }$ is 1.0 and Re is reduced from 800 to 500. Deceleration starts at t = 2400 and ends at t = 4800.
$\begin{figure} \epsfile{file=material/2-1/2-1-nc-01.eps,scale=1.0} \end{figure}$

**Figure:** Bifurcation from anomalous one-cell mode to normal one-cell mode and bifurcation from normal two-cell mode to anomalous one-cell mode. file=material/result/low-2.eps,scale=0.6 : lower limit of normal two-cell mode. file=material/result/high-1.eps,scale=0.6 : upper limit of anomalous one-cell mode. file=material/result/low-1.eps,scale=0.5 : lower limit of anomalous one-cell mode. file=material/result/high-2.eps,scale=0.6 : upper limit of normal two-cell mode. file=material/result/pfister.eps,scale=0.6 : numerically determined bifurcation (Cliffe, 1983).
$\begin{figure} \epsfile{file=material/result/result.eps,scale=0.98} \end{figure}$

**Figure:** Development of flow field from twin-cell mode to anomalous one-cell mode. ${\sl\Gamma }$ is 0.8 and Re is reduced from 1000 to 600. Deceleration starts at t = 3000 and ends at t = 6000.
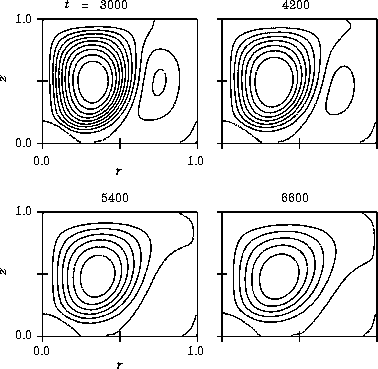
$\begin{figure} \epsfile{file=material/twin-1/twin-1-nc-01.eps,scale=1.0} \end{figure}$