HOME
クラスター分析とは、似ているものを集めて分類して、その中から意味のあるものを発見しようというデータマイニングの手法のひとつです。
細かい定義などは他に説明されているページがたくさんありますので、省略します。

クラスター分析には以下の７つの手法があります。分析手法の下に計算式を載せます。

以下の3手法に関しては次の式を用いて計算します。

dxc = αadxa + αbdxb + γ| dxa - dxb |

・最短距離法（最近隣法）[αa：0.5，αb：0.5，γ：-0.5]
dxc = 0.5dxa + 0.5dxb - 0.5| dxa - dxb |

・最長距離法（最遠隣法）[αa：0.5，αb：0.5，γ：0.5]
dxc = 0.5dxa + 0.5dxb + 0.5| dxa - dxb |

・群平均法[αa：na/nc，αb：nb/nc，γ：0]
dxc = (na/nc)dxa + (nb/nc)dxb + 0.5| dxa - dxb |

　

以下の4式には次の式を用いて計算します。
dxc

2

 = αadxa 2 + αbdxb 2 + βdab 2

・メディアン法 [αa：0.5，αb：0.5，β：-0.5]
dxc

2

 = 0.5dxa 2 + 0.5dxb 2 + 0.25dab 2

・重心法[αa：na/nc，αb：nb/nc，β：-((nanb)/nc]
dxc

2

 = (na/nc)dxa 2 + (nb/nc)dxb 2 -((nanb)/nc 2 )dab 2

・ウォード法[αa：(nx+na)/(nx+nc)，αb：(nx+nb)/(nx+nc)，β：nx/(nx+nc)]
dxc

2

 = ((nx+na)/(nx+nc))dxa 2 + ((nx+nb)/(nx+nc))dxb 2 + (nx/(nx+nc))dab 2

・可変法[αa：(1-β)/2，αb：(1-β)/2，β：β]
dxc

2

 = ((1-β)/2)dxa 2 + ((1-β)/2)dxb 2 + βdab 2

数式内の na はクラスターa に含まれる要素数を示しています。nb, nc, nx も同様です。
また、可変法内のβは１未満の任意の値を指定します。

ここでは最短距離法を用いてクラスター分析のアルゴリズムを説明していきたいと思います。

このページではクラスター分析プログラムを作るという観点から説明をしています。
こちらではアルゴリズムそのものについて説明しています。
アルゴリズムそのものにはあまり触れないので、分からない部分はアルゴリズムのページも見るいいかと思います。
A
B
C
D
E
A
-1
4
7
11.2
12.2
B
-
-1
8.1
7.8
9.2
C
-
-
-1
10.2
10
D
-
-
-
-1
2
E
-
-
-
-
-1

初期状態として、A,B,C,D,Eの座標があるとします。
A(2,8) B(6,8) C(2,1) D(12,3) E(12,1)
各座標間の距離は左記の行列のようになります。

ここで対角要素の値はA-A,B-B,C-C,D-D,E-Eの距離となります。よって距離は0なのですが、A-Aは同一のものなので
クラスター分析外の組み合わせであるため、プログラム上、距離が0であるものと区別するという意味で-1とします。
以下行列内の-1の値は分析対象外とします。

↓
A
B
C
D
E
A
-1
4
7
11.2
12.2
B
-
-1
8.1
7.8
9.2
C
-
-
-1
10.2
10
D
-
-
-
-1
-1
E
-
-
-
-
-1

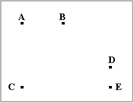
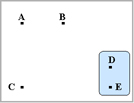
行列を調べると、座標D-E間が最も短いことが分かります。
よって、距離で考えると座標Dと座標Eの位置が最も似ていると判断し、
座標D,Eはひとつのグループを形成します。
ここでD,Eがひとつのグループとなったので距離を-1とします。

↓
A
B
C
D
E
A
-1
4
7
11.2
-1
B
-
-1
8.1
7.8
-1
C
-
-
-1
-1
10
D
-
-
-
-1
-1
E
-
-
-
-
-1

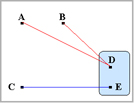
座標D,Eが同一グループを形成しているので、今までの座標D,E間に関する距離を計算しなおします。
最短距離法なので計算式は以下の式になります。ここでdxcのcはグループDEとなります。
dxc = 0.5dxa + 0.5dxb - 0.5| dxa - dxb |
これを用いると

dA(DE) = 0.5dAD + 0.5dAE - 0.5|dAD - dAE| = 0.5*11.2 + 0.5*12.2 - 0.5|11.2 - 12.2| = 11.2
dB(DE) = 0.5dBD + 0.5dBE - 0.5|dBD - dBE| = 0.5*7.8 + 0.5*9.2 - 0.5|7.8 - 9.2| = 7.8
dC(DE) = 0.5dCD + 0.5dCE - 0.5|dCD - dCE| = 0.5*10.2 + 0.5*10 - 0.5|10.2 - 10| = 10

各座標からのグループの代表点は上記の値となり、A-DE間の距離はA-DとなるためA-E=A-Dとしてもいいのですが、
A-Dがグループ化するということは、自動的にA-Eもグループ化するということなのでA-Eを分析対象から外します。
同様にB-E，C-Dも分析対象から外します。

↓
A
B
C
D
E
A
-1
-1
7
11.2
-1
B
-
-1
8.1
7.8
-1
C
-
-
-1
-1
10
D
-
-
-
-1
-1
E
-
-
-
-
-1

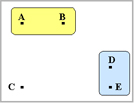
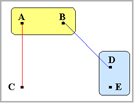
ここで、再び行列の中で最も短い距離の組み合わせを求めます。
最も距離の短い組み合わせはA-B間なので、今度はA-Bがグループを形成します。

ここではA-Bがグループを形成したのでA-B間の距離を-1とします。
↓
A
B
C
D
E
A
-1
-1
7
-1
-1
B
-
-1
-1
7.8
-1
C
-
-
-1
-1
10
D
-
-
-
-1
-1
E
-
-
-
-
-1

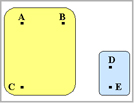
座標A,Bが同一グループを形成したので座標A,Bに関する距離を計算しなおします。
dxc = 0.5dxa + 0.5dxb - 0.5| dxa - dxb |　より

d(AB)c = 0.5dAC + 0.5dBC - 0.5|dAC - dBC| = 0.5*7 + 0.5*8.1 - 0.5|7 - 8.1| = 7
d(AB)(DE) = 0.5dA(DE) + 0.5dB(DE) - 0.5|dA(DE) - dB(DE)| = 0.5*11.2 + 0.5*7.8 -0.5|11.2 - 7.8| = 7.8
↓
A
B
C
D
E
A
-1
-1
-1
-1
-1
B
-
-1
-1
7.8
-1
C
-
-
-1
-1
10
D
-
-
-
-1
-1
E
-
-
-
-
-1

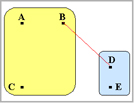
ここで、再び行列の中で最も短い距離の組み合わせを求めます。
最も距離の短い組み合わせはAB-C間なので、今度はAB-Cがグループを形成します。

ここではAB-Cがグループを形成したのでAB-C間の距離を-1とします。
↓
A
B
C
D
E
A
-1
-1
-1
-1
-1
B
-
-1
-1
7.8
-1
C
-
-
-1
-1
-1
D
-
-
-
-1
-1
E
-
-
-
-
-1

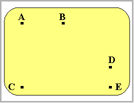
AB-Cが新たにグループABCを形成したので、ABC-DE間の距離を計算しなおします。
dxc = 0.5dxa + 0.5dxb - 0.5| dxa - dxb |　より

d(ABC)(DE) = 0.5d(AB)(DE) + 0.5dC(DE) - 0.5|d(AB)(DE) - dC(DE)| = 0.5*7.8 + 0.5*10 - 0.5|7.8 - 10| = 7.8
↓
A
B
C
D
E
A
-1
-1
-1
-1
-1
B
-
-1
-1
-1
-1
C
-
-
-1
-1
-1
D
-
-
-
-1
-1
E
-
-
-
-
-1
行列内で最も小さい組み合わせを探し、ABC-DEがグループABCDEを形成します。
ここで全てがひとつのグループとなり、クラスター分析はこれ以上できないので終了となります。