 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
-
|
-
|
-
|
-
|
|
B
|
-
|
0
|
-
|
-
|
-
|
|
C
|
-
|
-
|
0
|
-
|
-
|
|
D
|
-
|
-
|
-
|
0
|
-
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
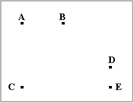
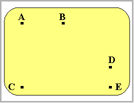
初期状態として、A,B,C,D,Eの座標があるとします。
ここでA〜Eの各xy座標は以下の通りです。
A(2,8)
B(6,8)
C(2,1)
D(12,3)
E(12,1)
|
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
4
|
7
|
11.2
|
12.2
|
|
B
|
-
|
0
|
8.1
|
7.8
|
9.2
|
|
C
|
-
|
-
|
0
|
10.2
|
10
|
|
D
|
-
|
-
|
-
|
0
|
2
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
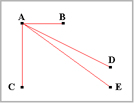
まず、座標Aから座標B,C,D,Eに対しての距離を求めます。
同様に座標Bから座標C,D,Eに対しての距離を求めます。
これを繰り返し、各座標間の全ての距離を求めます。
それによって作られる距離行列を左に示します。
この例では対称行列になるので上三角行列を用います。
|
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
4
|
7
|
11.2
|
12.2
|
|
B
|
-
|
0
|
8.1
|
7.8
|
9.2
|
|
C
|
-
|
-
|
0
|
10.2
|
10
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
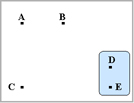
行列を調べると、座標D-E間が最も短いことが分かります。
よって、距離で考えると座標Dと座標Eの位置が最も似ていると判断し、
座標D,Eはひとつのグループを形成します。
ここでD,Eがひとつのグループとなったので距離を0とします。
以後座標はAのように表記し、 グループはDEのように2つ以上の座標を併せて表記します。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
4
|
7
|
11.2
|
0
|
|
B
|
-
|
0
|
8.1
|
7.8
|
0
|
|
C
|
-
|
-
|
0
|
0
|
10
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
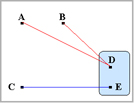
座標D,Eが同一グループを形成しているので、今までの座標D,E間に関する距離を計算しなおします。
ここでは最短距離法を用いて説明していますので、以下のように距離を更新します。
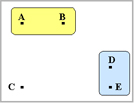
A-DE間の距離はA-D間,A-E間を比べ、A-D間が短いのでA-DE間はA-D間の距離となります。 (赤線)
B-DE間の距離はB-D間,B-E間を比べ、B-D間が短いのでB-DE間はB-D間の距離となります。 (赤線)
C-DE間の距離はC-D間,C-E間を比べ、C-E間が短いのでC-DE間はC-E間の距離となります。(青線)
これを行列に表すと左記のようになります。ここではA-D,A-E間の距離は同じクラスターへの距離となり、
同じ距離となるのでA-D間の距離のみを記しています。B-D,B-EとC-D,C-Eも同様です。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
0
|
7
|
11.2
|
0
|
|
B
|
-
|
0
|
8.1
|
7.8
|
0
|
|
C
|
-
|
-
|
0
|
0
|
10
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
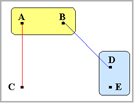
ここで、再び行列の中で最も短い距離の組み合わせを求めます。
最も距離の短い組み合わせはA-B間なので、今度はA-Bがグループを形成します。
ここではA-Bがグループを形成したのでA-B間の距離を0とします。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
0
|
7
|
0
|
0
|
|
B
|
-
|
0
|
0
|
7.8
|
0
|
|
C
|
-
|
-
|
0
|
0
|
0
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
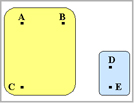
座標A,Bが同一グループを形成したので座標A,Bに関する距離を計算しなおします。
AB-C間の距離はA-C,B-Cを比べ、A-C間の距離が短いのでAB-C間の距離はA-C間の距離となります。(赤線)
AB-DE間の距離はA-D,A-E,B-D,B-E間の距離を比べ、B-D間が最も短いのでAB-DE間の距離は(青線)
B-D間の距離となります。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
0
|
0
|
0
|
0
|
|
B
|
-
|
0
|
0
|
7.8
|
0
|
|
C
|
-
|
-
|
0
|
0
|
0
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
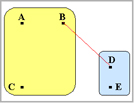
ここで、再び行列の中で最も短い距離の組み合わせを求めます。
最も距離の短い組み合わせはAB-C間なので、今度はAB-Cがグループを形成します。
ここではAB-Cがグループを形成したのでAB-C間の距離を0とします。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
0
|
0
|
0
|
0
|
|
B
|
-
|
0
|
0
|
7.8
|
0
|
|
C
|
-
|
-
|
0
|
0
|
0
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
AB-Cが新たにグループABCを形成したので、ABC-DE間の距離を計算しなおします。
以前と同様にABCとDEの各距離を求め、最も距離の短いB-D間がABC-DE間の距離となります。
|
|
|
↓
|
 |
|
|
A
|
B
|
C
|
D
|
E
|
|
A
|
0
|
0
|
0
|
0
|
0
|
|
B
|
-
|
0
|
0
|
0
|
0
|
|
C
|
-
|
-
|
0
|
0
|
0
|
|
D
|
-
|
-
|
-
|
0
|
0
|
|
E
|
-
|
-
|
-
|
-
|
0
|
|
行列内で最も小さい組み合わせを探し、ABC-DEがグループABCDEを形成します。
ここで、グループがひとつになったため、これ以上クラスター分析はできないので、ここで終了となります。 |
|








