| テーマ | 「回転場における流動現象のモード形成に関する研究」
内円筒が急激に増速するテイラー渦流れに関して、アスペクト比を1のオーダとしたとき、また、レイノルズ数を段階的に上げたときの、それぞれのモード形成過程と、準安定状態での最終モードについて、3次元数値解析により予測、検討しています。 |
| 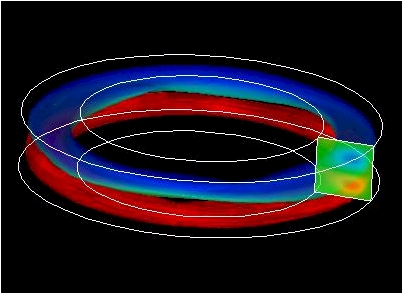
θ正方向に見て、赤色は時計周りの流れ、青色は反時計周りの流れを表します。
|
テーマを見たところで、すぐに理解できる人は…そうはいないでしょう…。
分かりやすく説明することにしましょう。
|
「テイラー渦とは?」
大きな円筒とその中に小さな円筒があり、2つに挟まれた空間には流体(水)が満たされています。いま、内円筒が回転を始めました。するとどうなるでしょう…。
内円筒の回転により、その付近の流体は遠心力を受け、外円筒方向へ押し出されます。当然、押し出されっぱなしでは状態平衡が保たれないので、流体には作用・反作用力が働き、外側へ押し出される一方で、内円筒側へ戻ってくる作用も起こります。これは渦を示すことになりますね。ビーカーの中の沸騰した水が、上昇後水面付近で2つに分岐して渦を起こす作用と似ていますね。
これがテイラー渦流れ(Taylor Couette FlowあるいはTaylor Vortexなど)と呼ばれている複雑系現象です。アスペクト比とはr-z断面における挟まれた空間(この場合は平面)の縦横比、レイノルズ数は内円筒の回転速度を表すパラメータです。これらパラメータや内円筒の増速具合によってモードの形成過程や最終モードが全く異なってきます。これを非一意性と呼び、テイラー渦に関する重要なキーワードであり、多くの研究者を悩ますところです。
|
「実際に、どういう研究をやってるのか?」
非一意性を実際に実験装置を使って解析しようとなると、時間と労力は計り知れません。
そこで私たちは、この現象の支配方程式であるNavier-Stokes方程式を解くコンピュータアルゴリズムを用いることにより、各条件下における数値結果を瞬時に出力し、それによりモードの形成や収束判定などを解析・検討しています。出力は数値なので、それが何を表すのかを理解するには、微分方程式理論の理解が必須になってきます。また「じゃあ、どうしてそのようなモードが現れるの?」と聞かれたときに、正確に理論を立てて説明できる力も必要になってきます。 |
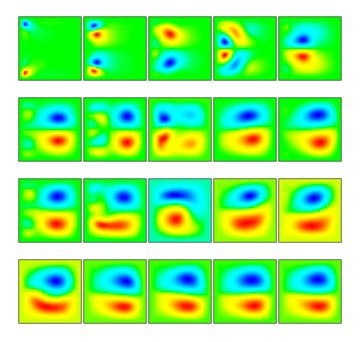
Figure アスペクト比 Γ =1.0 , レイノルズ数 Re =1300 のときのr-z断面
|

